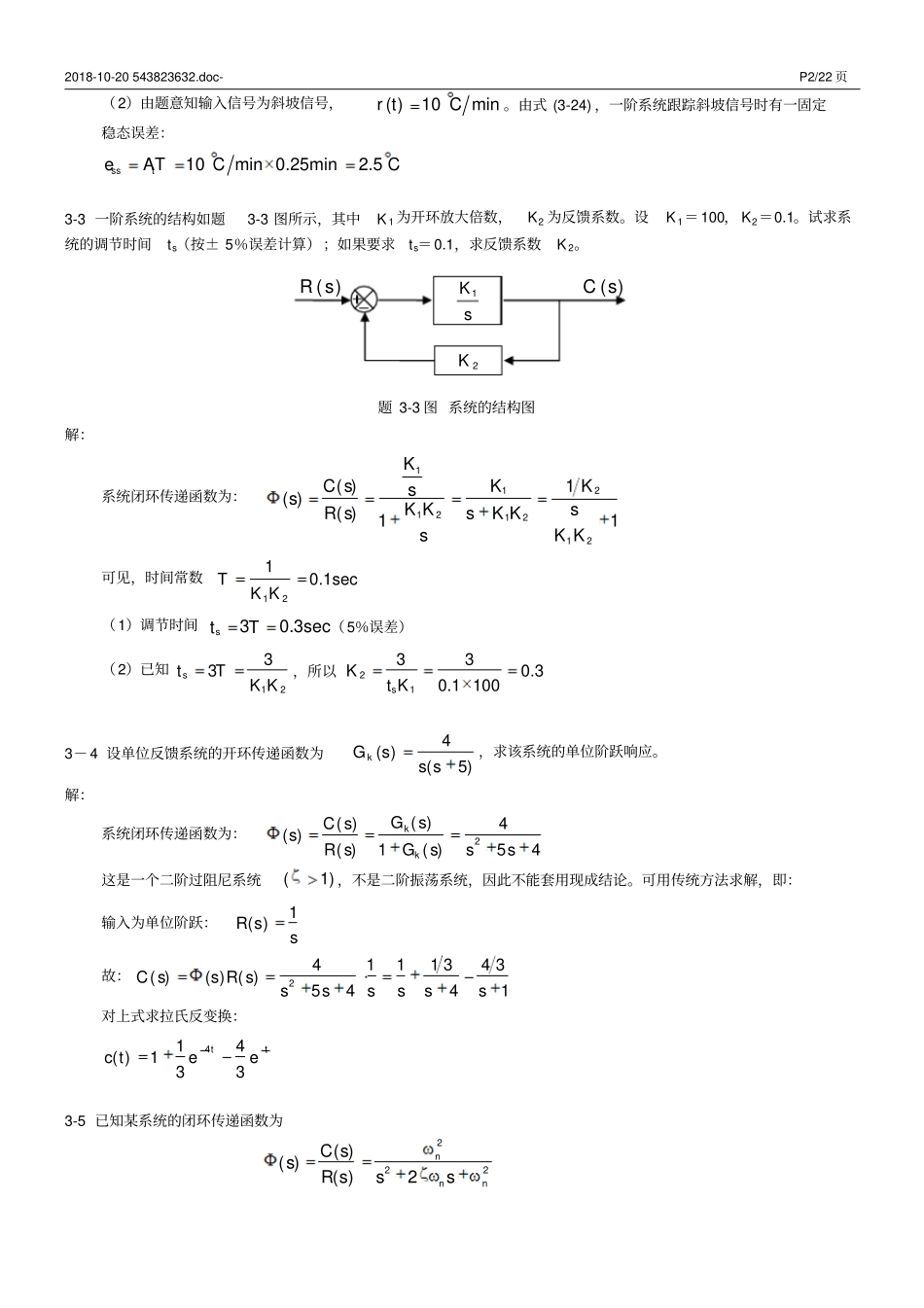
2018-10-20 543823632.doc- P1/22 页3-1 已知某单位反馈系统的开环传递函数为1)(TsKsG k,试求其单位阶跃响应。解法一,采用拉氏反变换:系统闭环传递函数为:( )( )( )( )1( )1kkGsC sKsR sGsTsK输入为单位阶跃,即:1( )R ss故:1( )( ) ( )11KABC ss R sKTsKsssT可由待定系数法求得:,11KKABKK所以,1111( )()111K KK KKC sKKsKsssTT对上式求拉氏反变换:1( )(1)1ktTKc teK解法二,套用典型一阶系统结论:由式 (3-15),已知典型一阶系统为:( )1( )( )1C ssR sTs由式 (3-16),其单位阶跃响应为:1( )1tTc te若一阶系统为( )( )( )1C sKsR sTs,则其单位阶跃响应为:1( )(1)tTc tKe现本系统闭环传递函数为:( )( )(1)( )( )1( )1(1)11kkGsC sKKKKsR sGsTsKTsKT s其中,,11TKTKKK所以,11( )(1)(1)1kttTTKc tKeeK采用解法二,概念明确且解题效率高,计算快捷且不易出错,应予提倡。3-2 设某温度计可用一阶系统表示其特性,现在用温度计测量容器中的水温,当它插入恒温水中一分钟时,显示了该温度的98%,试求其时间常数。又若给容器加热,水温由0℃按 10℃/min 规律上升,求该温度计的测量误差。解:(1)由题意知,误差为2%,因此调节时间:41minstT,即时间常数T:10.25min15 sec4sTt2018-10-20 543823632.doc- P2/22 页(2)由题意知输入信号为斜坡信号,( )10minr tC。由式 (3-24) ,一阶系统跟踪斜坡信号时有一固定稳态误差:10min 0.25min2.5ssteATCC3-3 一阶系统的结构如题3-3 图所示,其中K 1 为开环放大倍数,K2 为反馈系数。设K 1=100, K2=0.1。试求系统的调节时间ts(按± 5%误差计算);如果要求ts=0.1,求反馈系数K 2。题 3-3 图 系统的结构图解:系统闭环传递函数为:1121212121( )( )( )11KKKC sssK KsR ssK KK Ks可见,时间常数1210.1secTK K(1)调节时间30.3secstT(5%误差)(2)已知1233stTK K,所以21330.30.1 100sKt K3-4 设单位反馈系统的开环传递函数为)5(4)(sssG k,求该系统的单位阶跃响应。解:系统闭环传递函数为:2( )( )4( )( )1( )54kkGsC ssR sGsss这是一个二阶过阻尼系统(1) ,不是二阶振荡系统,因此不能套用现成结论。可用传统方法求解,即:输入为单位阶跃:1( )R ss故:24111 34 3( )( ) ( )5441C ss R sssssss对上式求拉氏反变换:tteetc34311)(43-5 已知某系统的闭环传递函数为22...