6事件的关系和运算 高二数学选修2-3从排列组合到正态分布全部课件一 新课标 高二数学选修2-3从排列组合到正态分布全部课件一 新课标VIP免费

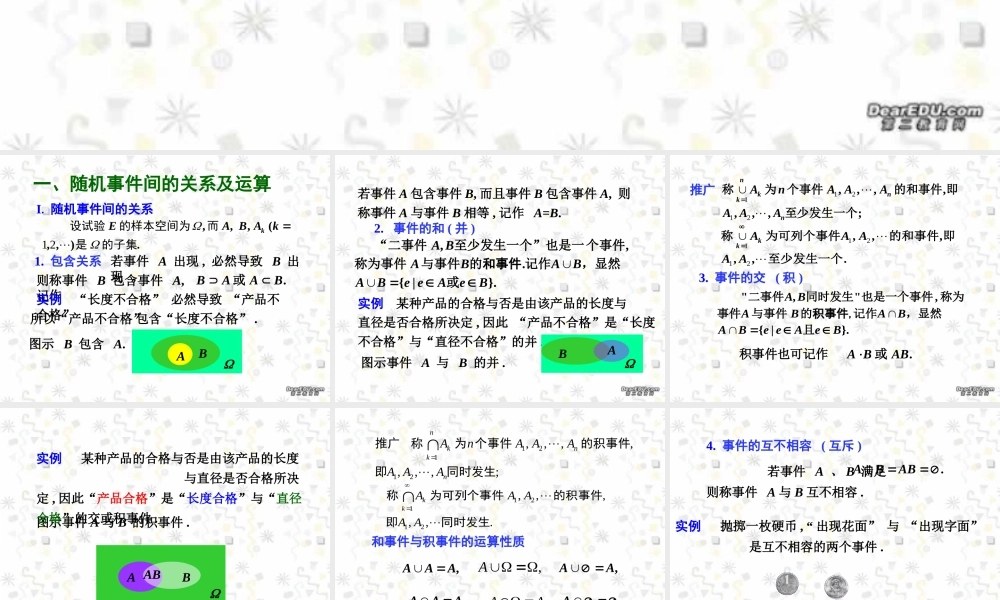
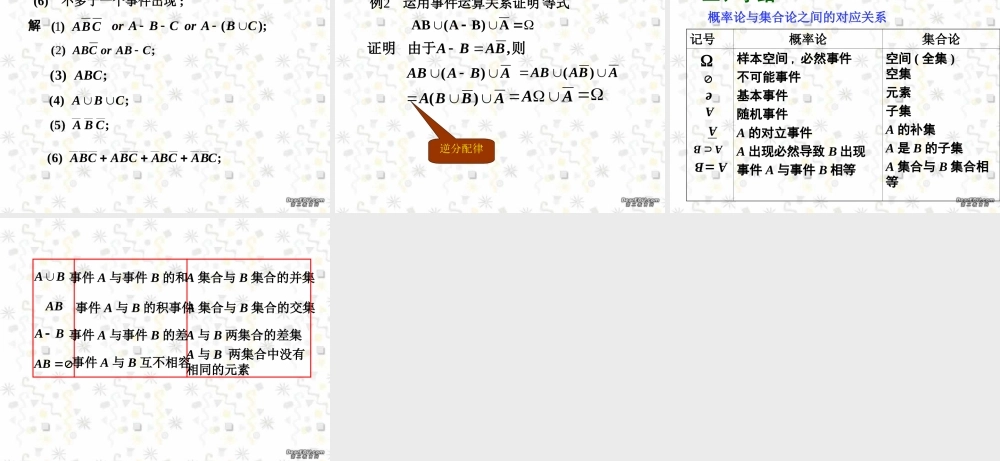
一、随机事件间的关系及运算第 1.2 节 事件的关系和运算二、小结.),,( , , ,的子集是而的样本空间为设试验21kABAEk 1. 包含关系 若事件 A 出现 , 必然导致 B 出现 ,则称事件 B 包含事件 A,记作.BAAB或实例 “长度不合格” 必然导致 “产品不合格”所以“产品不合格”包含“长度不合格” .图示 B 包含 A.BA一、随机事件间的关系及运算I. 随机事件间的关系若事件 A 包含事件 B, 而且事件 B 包含事件 A, 则称事件 A 与事件 B 相等 , 记作 A=B.2. 事件的和 ( 并 )}.|{. ,,BeAeeBABABABA或，显然记作的与事件称为事件个事件至少发生一个”也是一“二事件和事件实例 某种产品的合格与否是由该产品的长度与直径是否合格所决定 , 因此 “产品不合格”是“长度不合格”与“直径不合格”的并 .图示事件 A 与 B 的并 . BA;,,,, , , , 至少发生一个即的和事件个事件为称nnknkAAAAAAnA212113. 事件的交 ( 积 ).ABBA或积事件也可记作.,,, , ,至少发生一个即的和事件为可列个事件称21211AAAAAkk}.|{ ,","BeAeeBABABABA且，显然记作的与事件事件称为也是一个事件同时发生二事件积事件,推广图示事件 A 与 B 的积事件 .ABAB实例 某种产品的合格与否是由该产品的长度 与直径是否合格所决定 , 因此“产品合格”是“长度合格”与“直径合格”的交或积事件 .和事件与积事件的运算性质,AAA, A,AA,AAA,AA.A;,,,, , , ,21211同时发生即的积事件个事件为称推广nnnkkAAAAAAnA.,,, , ,21211同时发生即的积事件为可列个事件称AAAAAkk4. 事件的互不相容 ( 互斥 ) 若事件 A 、 B 满足则称事件 A 与 B 互不相容 ..ABBA 实例 抛掷一枚硬币 , “ 出现花面” 与 “出现字面” 是互不相容的两个事件 .“ 骰子出现 1 点” “骰子出现 2 点”图示 A 与 B互斥AB互斥实例 抛掷一枚骰子 , 观察出现的点数 . 说明 当 AB=  时 , 可将 AB 记为“直和”形式 A+B. 任意事件 A 与不可能事件为互斥 .5. 事件的差图示 A 与 B 的差ABBAB AB BABA 实例 “长度合格但直径不合格”是“长度合格” 与“直径合格”的差 .A事件 “ A 出现而 B 不出现”，称为事件 A 与 B 的差 . 记作 A-...