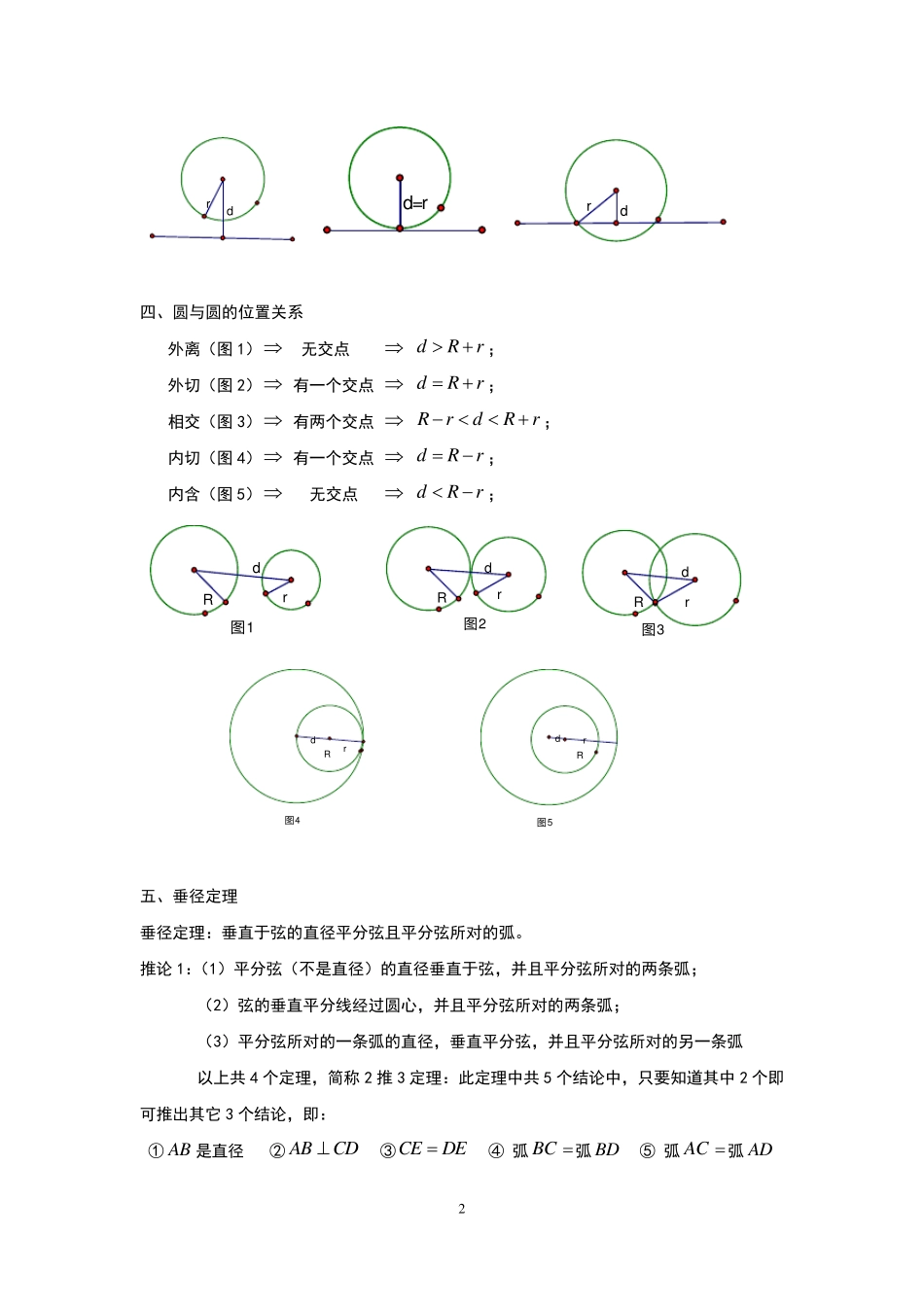
1 《圆》章节知识点复习 圆的记忆口诀: 常把半径直径连,有弦可做弦心距,它定垂直平分弦,直圆周角立上边。 圆有内接四边形,对角互补记心间,外角等于内对角,四边形定内接圆, 直角相对成共弦,试试加一个辅助圆,若是证题打转轴,四点共圆可解难, 要想证明圆切线,垂直半径过外端,直线与圆有共点,证垂直来半径连 直线与圆未给点,需证半径作垂线,四边形有内切圆,对边和等是条件, 如果遇到圆与圆,弄清位置很关键,圆相切做公切,两圆想交连工弦。 一、圆的概念 集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合; 轨迹形式的概念: 1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; 2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内 dr 点C 在圆内; 2、点在圆上 dr 点B 在圆上; 3、点在圆外 dr 点A 在圆外; 三、直线与圆的位置关系 1、直线与圆相离 dr 无交点; 2、直线与圆相切 dr 有一个交点; 3、直线与圆相交 dr 有两个交点; rddCBAO2 四、圆与圆的位置关系 外离(图1) 无交点 dRr; 外切(图2) 有一个交点 dRr; 相交(图3) 有两个交点 RrdRr ; 内切(图4) 有一个交点 dRr; 内含(图5) 无交点 dRr; 五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4 个定理,简称2 推3 定理:此定理中共5 个结论中,只要知道其中2 个即可推出其它3 个结论,即: ① AB 是直径 ② ABCD ③CEDE ④ 弧BC 弧BD ⑤ 弧AC 弧AD drd=rrd图1rRd图3rRd图2rRd图4rRd图5rRd3 中任意2 个条件推出其他3 个结论。 推论2:圆...