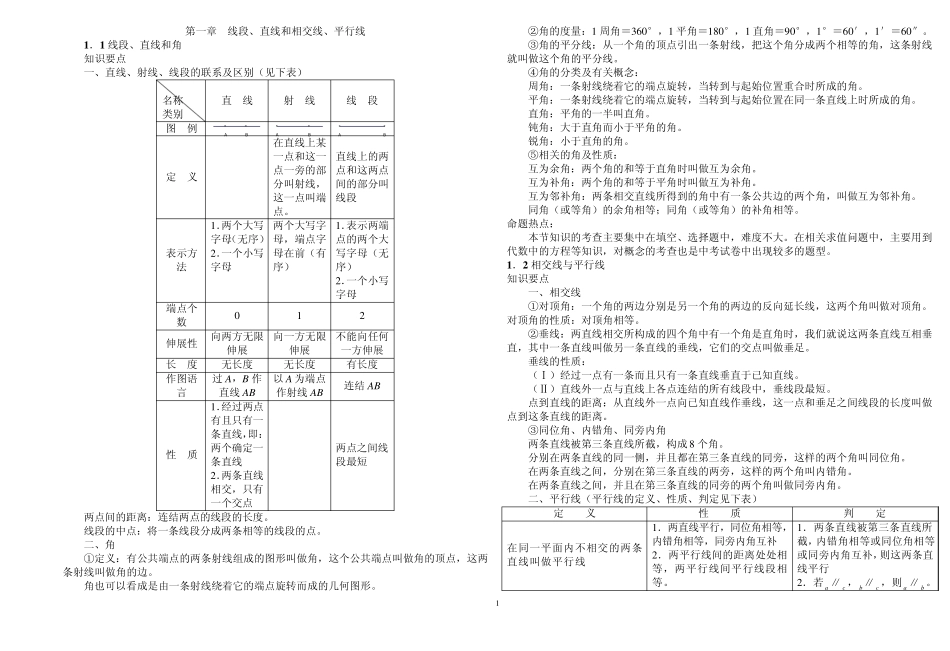
1 第一章 线段、直线和相交线、平行线 1 .1 线段、直线和角 知识要点 一、直线、射线、线段的联系及区别(见下表) 名称 类别 直 线 射 线 线 段 图 例 AB AB AB 定 义 在直线上某一点和这一点一旁的部分叫射线,这一点叫端点。 直线上的两点和这两点间的部分叫线段 表示方法 1 .两个大写字母(无序) 2 .一个小写字母 两个大写字母,端点字母在前(有序) 1 .表示两端点的两个大写字母(无序) 2 .一个小写字母 端点个数 0 1 2 伸展性 向两方无限伸展 向一方无限伸展 不能向任何一方伸展 长 度 无长度 无长度 有长度 作图语言 过A,B 作直线AB 以A 为端点作射线AB 连结AB 性 质 1 .经过两点有且只有一条直线,即:两个确定一条直线 2 .两条直线相交,只有一个交点 两点之间线段最短 两点间的距离:连结两点的线段的长度。 线段的中点:将一条线段分成两条相等的线段的点。 二、角 ①定义:有公共端点的两条射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。 角也可以看成是由一条射线绕着它的端点旋转而成的几何图形。 ②角的度量:1 周角=3 6 0 °,1 平角=1 8 0 °,1 直角=9 0 °,1 °=6 0 ′,1 ′=6 0 ″。 ③角的平分线:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线就叫做这个角的平分线。 ④角的分类及有关概念: 周角:一条射线绕着它的端点旋转,当转到与起始位置重合时所成的角。 平角:一条射线绕着它的端点旋转,当转到与起始位置在同一条直线上时所成的角。 直角:平角的一半叫直角。 钝角:大于直角而小于平角的角。 锐角:小于直角的角。 ⑤相关的角及性质: 互为余角:两个角的和等于直角时叫做互为余角。 互为补角:两个角的和等于平角时叫做互为补角。 互为邻补角:两条相交直线所得到的角中有一条公共边的两个角,叫做互为邻补角。 同角(或等角)的余角相等;同角(或等角)的补角相等。 命题热点: 本节知识的考查主要集中在填空、选择题中,难度不大。在相关求值问题中,主要用到代数中的方程等知识,对概念的考查也是中考试卷中出现较多的题型。 1 .2 相交线与平行线 知识要点 一、相交线 ①对顶角:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。对顶角的性质:对顶角相等。 ②垂线:两直线相交所构成的四个角中有一个角是...