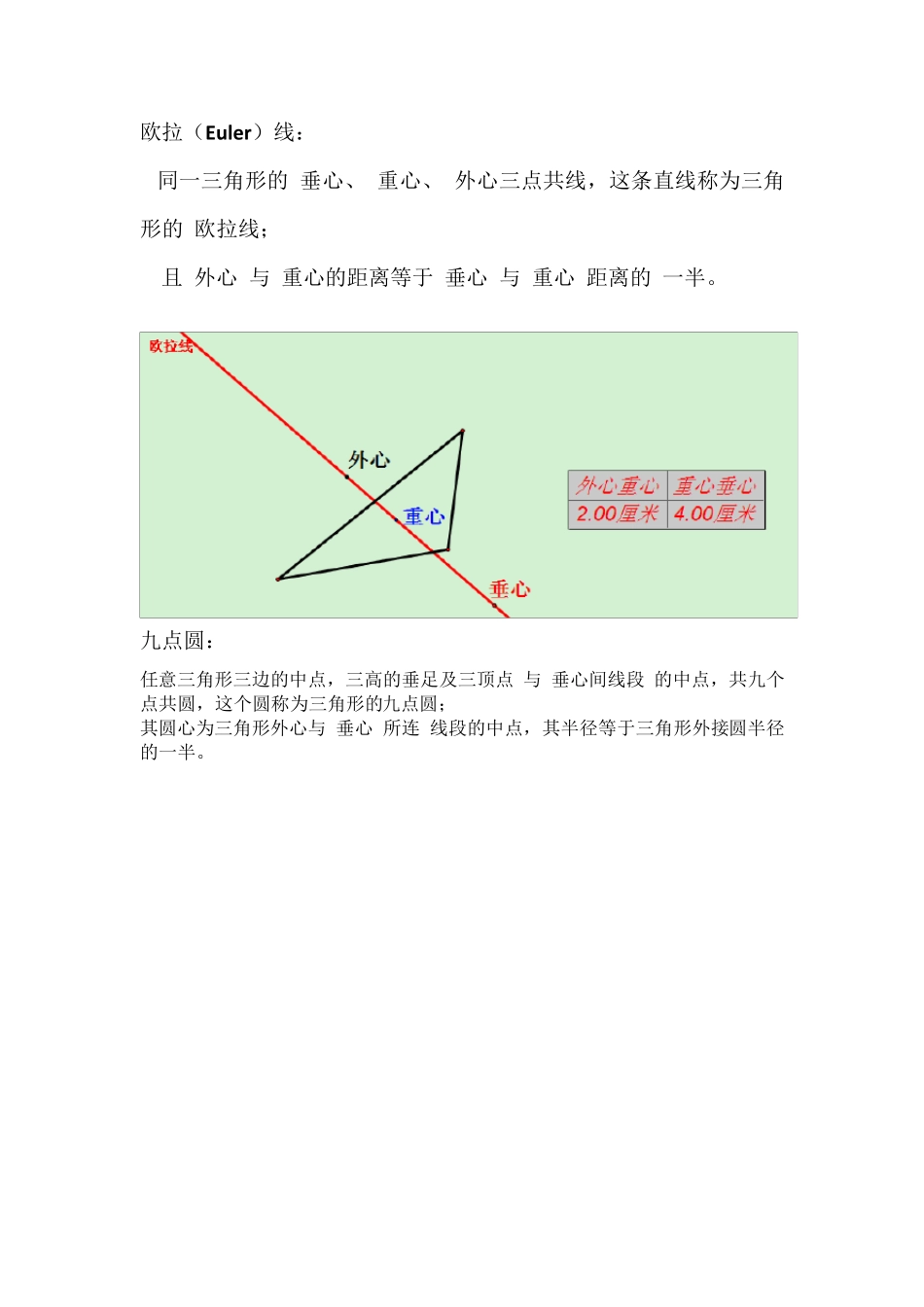
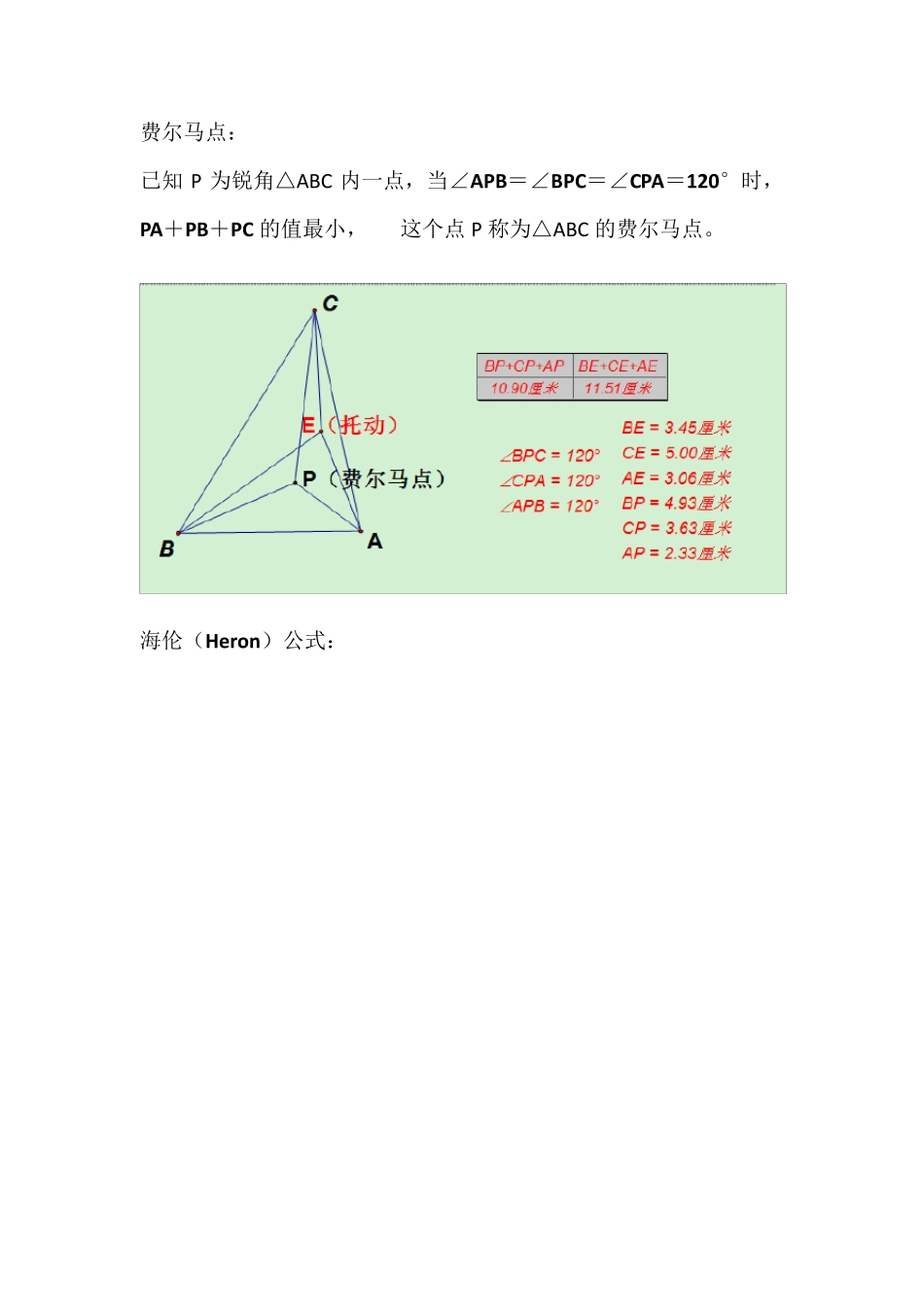
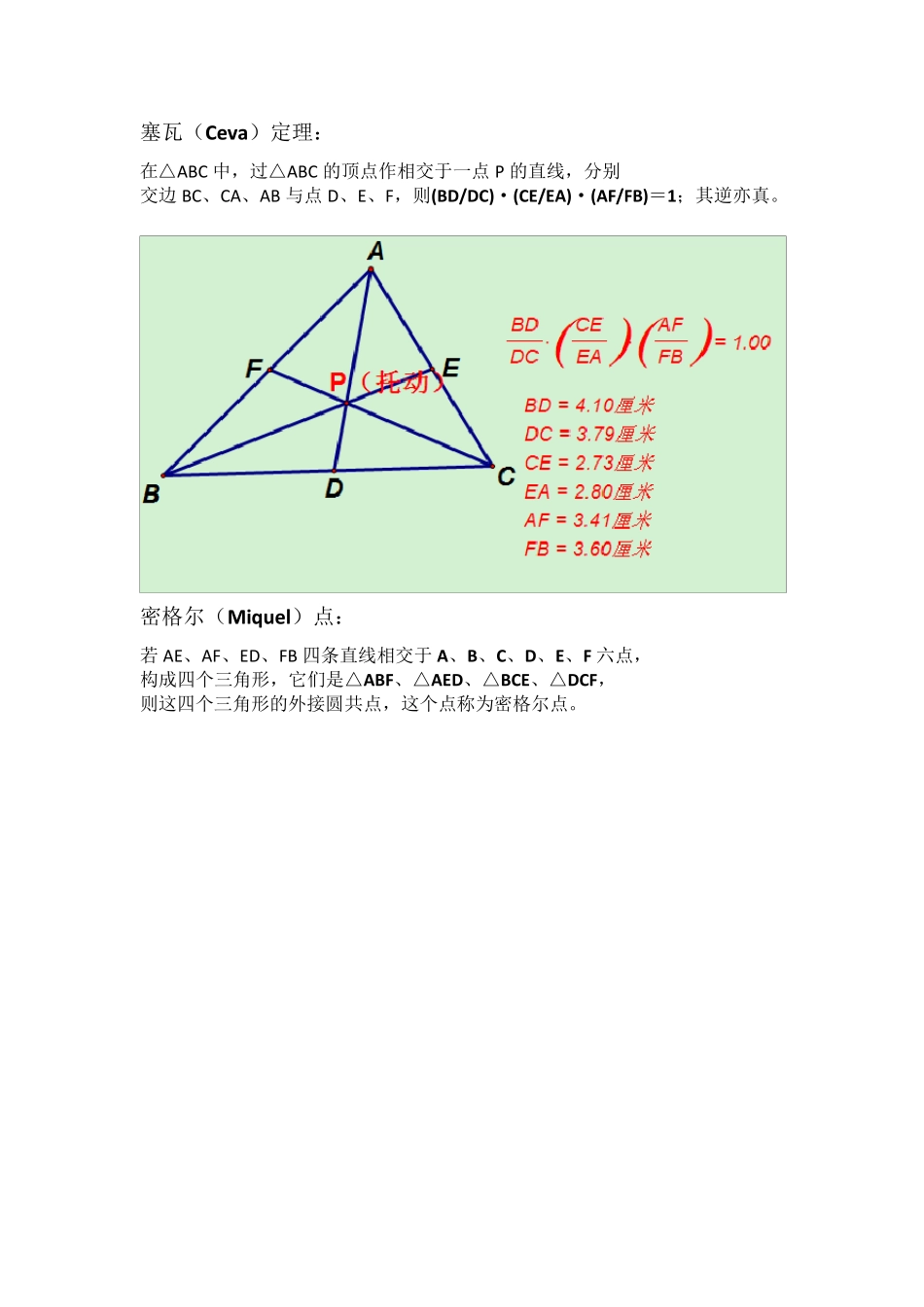
欧拉(Eu ler)线: 同一三角形的 垂心、 重心、 外心三点共线,这条直线称为三角形的 欧拉线; 且 外心 与 重心的距离等于 垂心 与 重心 距离的 一半。 九点圆: 任意三角形三边的中点,三高的垂足及三顶点 与 垂心间线段 的中点,共九个点共圆,这个圆称为三角形的九点圆; 其圆心为三角形外心与 垂心 所连 线段的中点,其半径等于三角形外接圆半径的一半。 费尔马点: 已知P 为锐角△ABC 内一点,当∠APB=∠BPC=∠CPA=120°时,PA+PB+PC 的值最小, 这个点P 称为△ABC 的费尔马点。 海伦(Heron)公式: 塞瓦(Ceva)定理: 在△ABC 中,过△ABC 的顶点作相交于一点P 的直线,分别 交边BC、CA、AB 与点D、E、F,则(BD/DC)·(CE/EA)·(AF/FB)=1;其逆亦真。 密格尔(Miquel)点: 若 AE、AF、ED、FB 四条直线相交于A、B、C、D、E、F 六点, 构成四个三角形,它们是△ABF、△AED、△BCE、△DCF, 则这四个三角形的外接圆共点,这个点称为密格尔点。 葛尔刚(Gergonne)点: △ABC 的内切圆分别切边AB、BC、CA 于点D、E、F, 则AE、BF、CD 三线共点,这个点称为葛尔刚点。 西摩松(Simson)线: 已知P 为△ABC 外接圆周上任意一点,PD⊥BC,PE⊥ACPF⊥AB,D、E、F 为垂足, 则D、E、F 三点共线,这条直线叫做西摩松线。 黄金分割: 把一条线段(AB)分成两条线段,使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项,这样的分割称为黄金分割。 帕普斯(Pappus)定理: 已知点A1、A2、A3 在直线l1 上,已知点B1、B2、B3 在直线l2 上, 且 A1 B2 与A2 B1 交于点X,A1B3 与A3 B1 交于点Y,A2 B3 于 A3 B2 交于 点Z,则 X、Y、Z 三点共线。 笛沙格(Desargues)定理: 已知在△ ABC 与△A'B'C'中,AA'、BB'、CC'三线相交于点 O, BC 与 B'C'、CA 与 C'A'、AB 与 A'B'分别相交于点 X、Y、Z,则 X、Y、Z 三点共线;其逆亦真 摩莱(Morley)三角形: 在已知△ABC 三内角的三等分线中,分别与 BC、CA、AB 相邻的每两线相交于点 D、E、F,则△DEF 是正三角形, 这个正三角形称为摩莱三角形。 帕斯卡(Paskal)定理: 已知圆内接六边形ABCDEF 的边AB、DE 延长线交于点G,边BC、EF延长线交于点H,边CD、FA 延长线交于点K ,则H、G、K 三点共线。 托勒密(Ptolemy)定理: 在圆内接四边形中,AB·CD+AD·BC=AC·BD (...