矩阵习题答案VIP免费

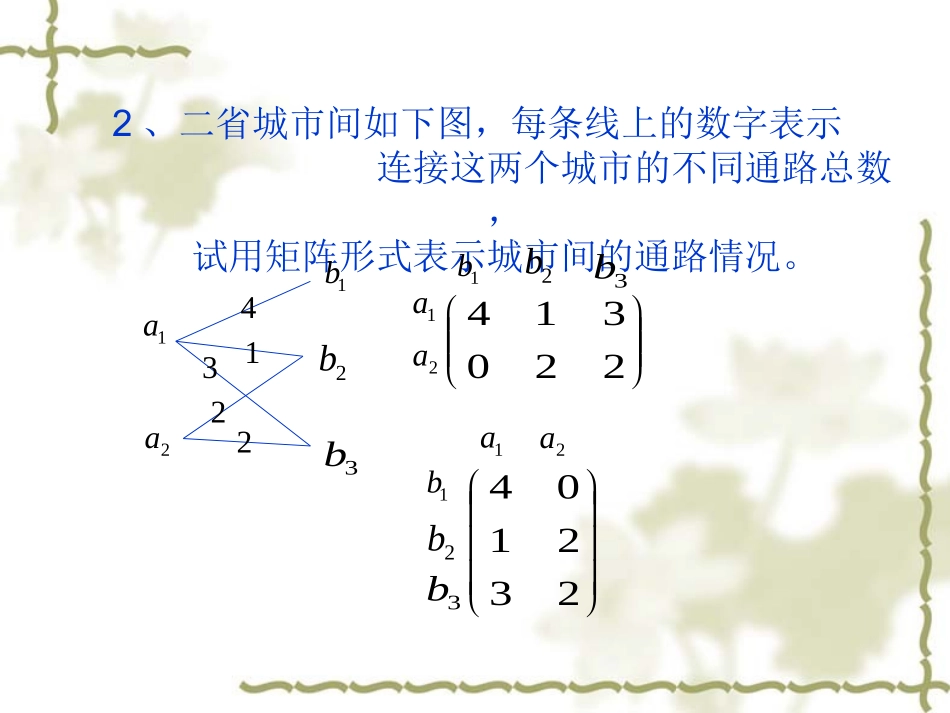
第一章矩阵。11,yxyx,cossinsincos)2(000)1(1111yxyyxxyxyyxx1、写出下列由变量到变量的线性变换的系数矩阵：0001AcossinsincosA2、二省城市间如下图，每条线上的数字表示连接这两个城市的不同通路总数，试用矩阵形式表示城市间的通路情况。1a2a1b3b2b1a2a1b2b3b2203141b2b3b1a2a23210422413,111111111A,150421321BAAB23BAT229420172221320926508503.4、计算2210013112)1(11)2(212222111211yxcbbbaabaayx433349447ybxbxyacyaxa2112222211222ybxbxyacyaxa12122121122222211zyxaaaaaaaaazyx333231232221131211yzaaxzaaxyaazayaxa)()()(322331132112233222211补充5、已知两个线性变换32133212311542322yyyxyyyxyyx,323323312211zzyzzyzzy321,,zzz321,,xxx求从到的线性变换,AYX,BZYABZX514232102A310102013B161109412316AB,1610941236321332123211zzzxzzzxzzzx所以分析：6.设,)(10mmmaxaxaxf是阶方阵，An定义,)(10EaAaAaAfmmm,35)(2xxxf3312A)(Af当时，求解：EAAAf35)(222O7.设方阵A满足证明：AEA2,232OEAAA都可逆，分别表示出它们的为可逆矩阵。及并用证明：EAA232EAEA2)3(EAEA)3(21)3(211EAAEEAAEA4)2()2(,4222OEEAAAEEAEA4))(2(EEAEA)(21)2(1)2(EA8.利用初等行变换把下列矩阵化成行最简形矩阵：132126421321)1(A122rr13rr00000000132103341431210110122413)2(B0334143121224130110112rr02240422202111001101123rr13rr14rr022404222021110011012)1(r86200000002111001101232rr244rr00000431002111001101421r43rr0000043100220104400132rr31rr9.对下列初等行变换，写出相应的初等方阵以及和之间的关系式。AB121121322101A~122rr121123302101~13ccB1311233020011000100013E~122rrP10001200110000100001000014E~13ccQ1000010000100101BPAQ10.设,1APP其中2001,1141P求9A提示：1PPA111919)(PPPPPPPPA19PP11.设,200030004ABAAB2求B提示：ABEA)2(AEAB11)2(方法一：先求,)2(1EAAEA1)2(再求方法二：直接求AEA1)2())2((AEA))2((1AEAE行41000100021)2(1EA210003000220003000441000100021B其中12.设,1210102312202321A利用初等行变换求1A)(EA10001210010010230010122000012321~...