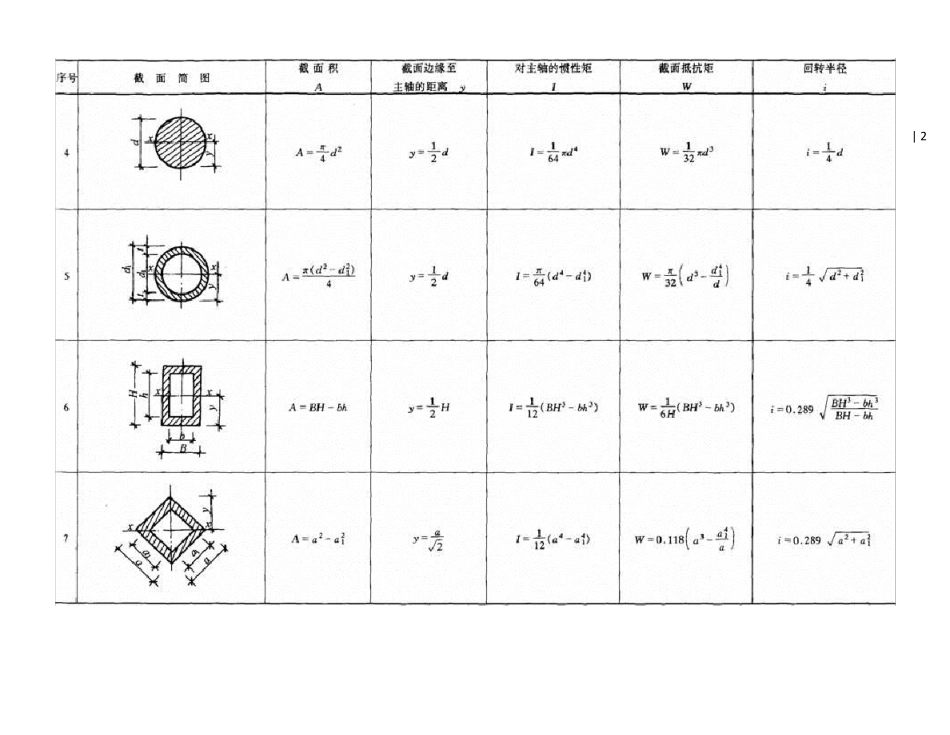
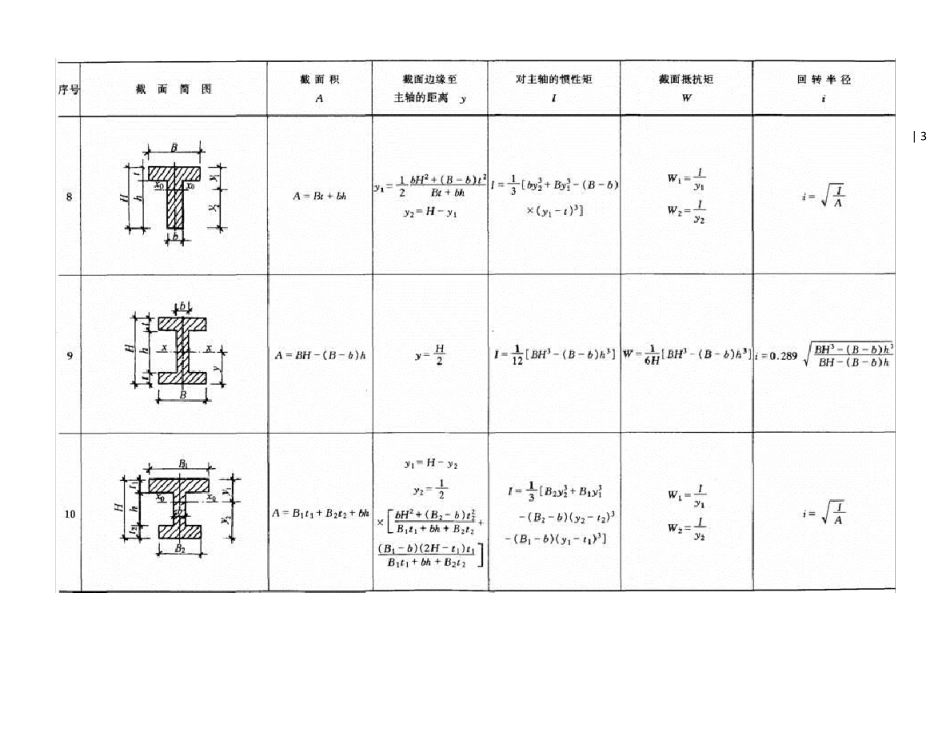
| 1 常用截面几何与力学特征表 | 2 | 3 | 4 | 5 | 6 | 7 注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm4)。基本计算公式如下: 2.W 称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下: 3.i 称截面回转半径(mm),其基本计算公式如下: 4.上列各式中,A 为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I 为对主轴(形心轴)的惯性矩。 5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。 | 8 单跨梁的内力及变形表(1)简支梁的反力、剪力、弯矩、挠度 | 9 | 10 | 11 (2)悬臂梁的反力、剪力、弯矩和挠度 | 12 | 13 (3)一端简支另一端固定梁的反力、剪力、弯矩和挠度 | 14 | 15 | 16 (4)两端固定梁的反力、剪力、弯矩和挠度 | 17 | 18 | 19 (5)外伸梁的反力、剪力、弯矩和挠度 | 20 | 21 | 22 | 23 等截面连续梁的内力及变形表 二跨等跨梁的内力和挠度系数 注:1.在均布荷载作用下:M=表中系数×q l2;V=表中系数×q l;w =表中系数×q l4/(100EI)。 2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;w =表中系数×Fl3/(100EI)。 [例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。 [解] MB 支=(-0.125×11.76×52)+(-0.188×29.4×5) =(-36.75)+(-27.64)=-64.39kN·m VB 左=(-0.625×11.76×5)+(-0.688×29.4) =(-36.75)+(-20.23)=-56.98kN [例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。 [解] M1=0.080×11.76×62=33.87kN·m。 | 24 不等跨连续梁的内力系数1)二不等跨梁的内力系数 注:1.M=表中系数×q l21;V=表中系数×q l1; 2.(Mmax)、(Vmax)表示它为相应跨内的最大内力。 | 25 2)三不等跨梁内力系数 注:1.M=表中系数×q l21;V=表中系数×q l1; 2.(Mmax)、(Vmax)为荷载在最不利布置时的最大内力。 | 26 “┌┐”形刚架内力计算表 (一) | 27 | 28 “┌┐”形刚架内力计算表(二) | 29 | 30 “”形刚架的内力计算表 | 31 | 32