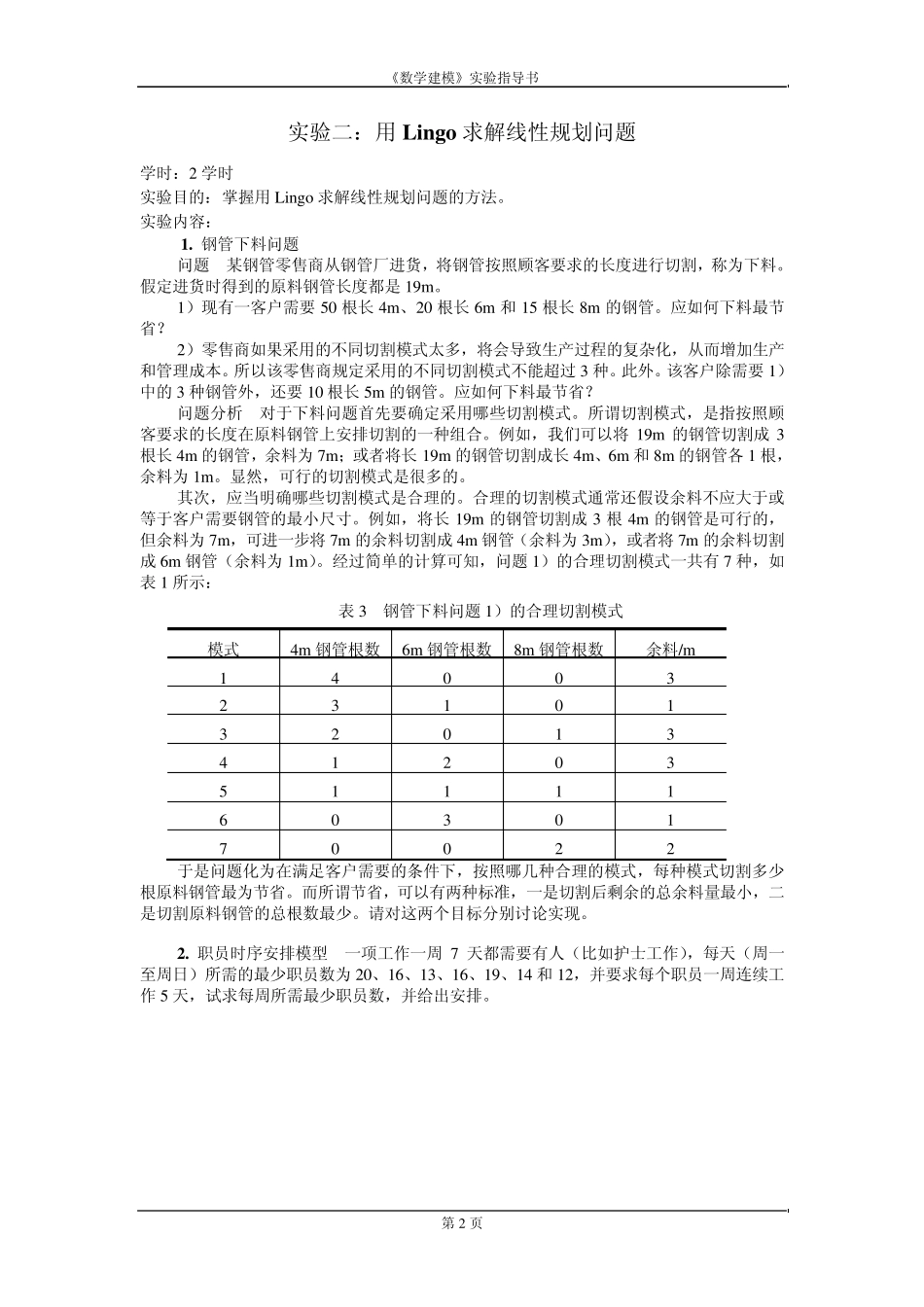
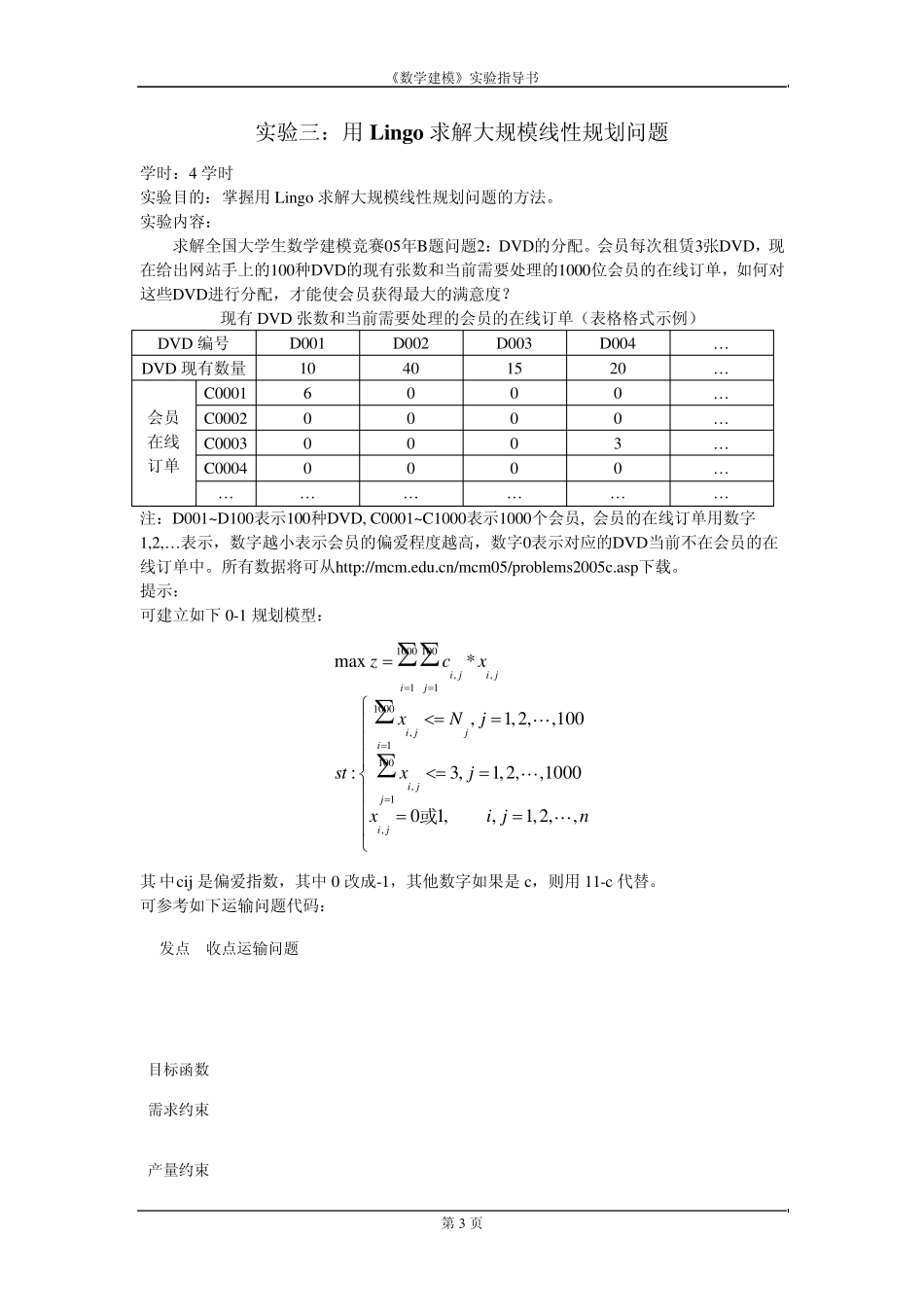
《数学建模》实验指导书 第1 页 《数学建模》实验指导书 实验一:matlab 编程基础 学时:2 学时 实验目的:熟悉matlab 编程 实验内容: 1. f(x )的定义如下: 2226,04( )56,010,231,xxxxf xxxxxxxx 且且其它 写一个函数文件f(x )实现该函数,要求参数x 可以是向量。 2. 用起泡法对10 个数由小到大排序. 即将相邻两个数比较,将小的调到前头. 3. 有一个45矩阵,编程求出其最大值及其所处的位置. 4. 编程求201!nn 5. 一球从100 米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10 次反弹有多高? 6. 有一函数 ,写一程序,输入自变量的值,输出函数值. 7. 写一个函数rs=f(s),对传进去的字符串变量s,删除其中的小写字母,然后将原来的大写字母变为小写字母,得到rs 返回。例如s=”aBcdE,Fg?”,则 rs=”be,f?”。提示:可利用find 函数和空矩阵。 2( , )sin2f x yxxyy《数学建模》实验指导书 第2 页 实验二:用Lingo 求解线性规划问题 学时:2 学时 实验目的:掌握用Lingo求解线性规划问题的方法。 实验内容: 1. 钢管下料问题 问题 某钢管零售商从钢管厂进货,将钢管按照顾客要求的长度进行切割,称为下料。假定进货时得到的原料钢管长度都是19m。 1)现有一客户需要50 根长4m、20 根长6m 和 15 根长8m 的钢管。应如何下料最节省? 2)零售商如果采用的不同切割模式太多,将会导致生产过程的复杂化,从而增加生产和管理成本。所以该零售商规定采用的不同切割模式不能超过 3 种。此外。该客户除需要1)中的3 种钢管外,还要10 根长5m 的钢管。应如何下料最节省? 问题分析 对于下料问题首先要确定采用哪些切割模式。所谓切割模式,是指按照顾客要求的长度在原料钢管上安排切割的一种组合。例如,我们可以将19m 的钢管切割成 3根长4m 的钢管,余料为7m;或者将长19m 的钢管切割成长4m、6m 和 8m 的钢管各 1 根,余料为1m。显然,可行的切割模式是很多的。 其次,应当明确哪些切割模式是合理的。合理的切割模式通常还假设余料不应大于或等于客户需要钢管的最小尺寸。例如,将长19m 的钢管切割成 3 根4m 的钢管是可行的,但余料为7m,可进一步将7m 的余料切割成 4m 钢管(余料为3m),或者将7m 的余料切割成 6m 钢管(余料为1m)。经过简单的计算可知,问题1)的...