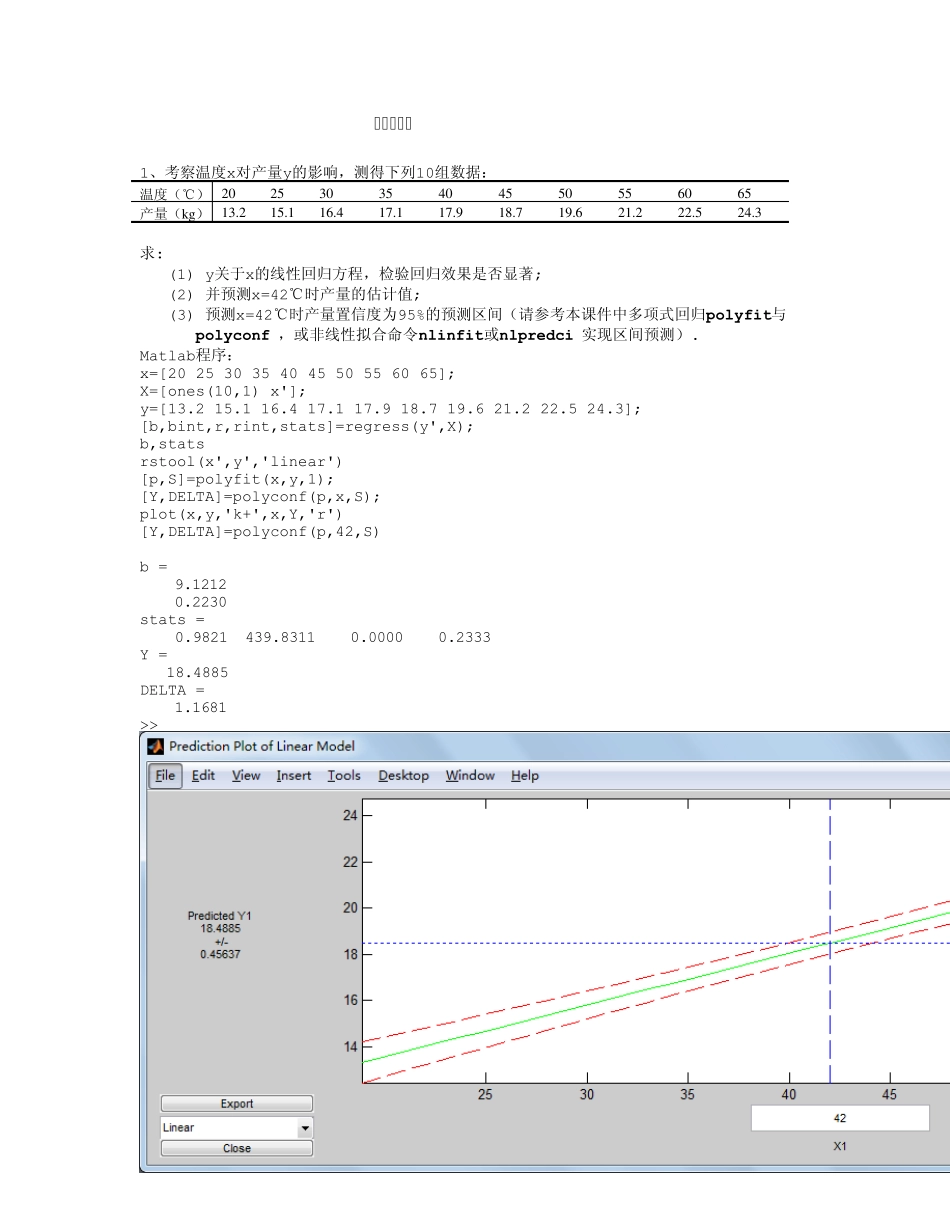
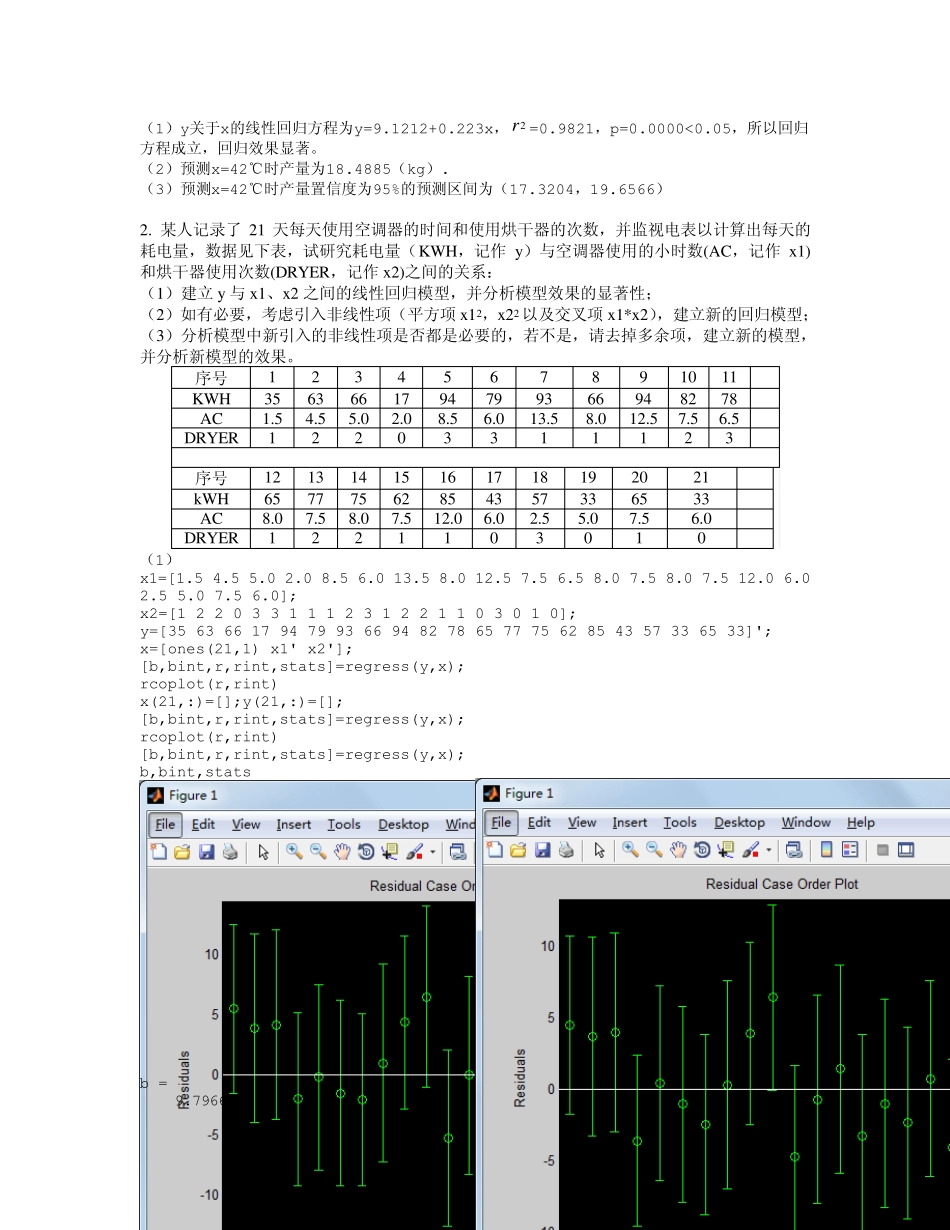
统计与回归 1、考察温度x对产量y的影响,测得下列10组数据: 温度(℃) 2 0 2 5 3 0 3 5 4 0 4 5 5 0 5 5 6 0 6 5 产量(k g ) 1 3 .2 1 5 .1 1 6 .4 1 7 .1 1 7 .9 1 8 .7 1 9 .6 2 1 .2 2 2 .5 2 4 .3 求: (1) y关于x的线性回归方程,检验回归效果是否显著; (2) 并预测x=42℃时产量的估计值; (3) 预测x=42℃时产量置信度为95%的预测区间(请参考本课件中多项式回归polyfit与polyconf ,或非线性拟合命令nlinfit或nlpredci 实现区间预测). Matlab程序: x=[20 25 30 35 40 45 50 55 60 65]; X=[ones(10,1) x']; y=[13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3]; [b,bint,r,rint,stats]=regress(y',X); b,stats rstool(x',y','linear') [p,S]=polyfit(x,y,1); [Y,DELTA]=polyconf(p,x,S); plot(x,y,'k+',x,Y,'r') [Y,DELTA]=polyconf(p,42,S) b = 9.1212 0.2230 stats = 0.9821 439.8311 0.0000 0.2333 Y = 18.4885 DELTA = 1.1681 >> (1)y关于x的线性回归方程为y=9.1212+0.223x,2r =0.9821,p=0.0000<0.05,所以回归方程成立,回归效果显著。 (2)预测x=42℃时产量为18.4885(kg). (3)预测x=42℃时产量置信度为95%的预测区间为(17.3204,19.6566) 2. 某人记录了 21 天每天使用空调器的时间和使用烘干器的次数,并监视电表以计算出每天的耗电量,数据见下表,试研究耗电量(KWH,记作 y)与空调器使用的小时数(AC,记作 x1)和烘干器使用次数(DRYER,记作 x2)之间的关系: (1)建立y与 x1、x2 之间的线性回归模型,并分析模型效果的显著性; (2)如有必要,考虑引入非线性项(平方项 x12,x22 以及交叉项 x1*x2),建立新的回归模型; (3)分析模型中新引入的非线性项是否都是必要的,若不是,请去掉多余项,建立新的模型,并分析新模型的效果。 序号 1 2 3 4 5 6 7 8 9 10 11 KWH 35 63 66 17 94 79 93 66 94 82 78 AC 1.5 4.5 5.0 2.0 8.5 6.0 13.5 8.0 12.5 7.5 6.5 DRYER 1 2 2 0 3 3 1 1 1 2 3 序号 12 13 14 15 16 17 18 19 20 21 kWH 65 77 75 62 85 43 57 33 65 33 AC 8.0 7.5 8.0 7.5 12.0 6.0 2.5 5.0 7.5 6.0 DRYER 1 2 2 1 1 0 3 0 1 0 (1) x1=[1.5 4.5 5.0 2.0 8....