数值计算技巧Matlab实题训练内附程序,模型VIP免费

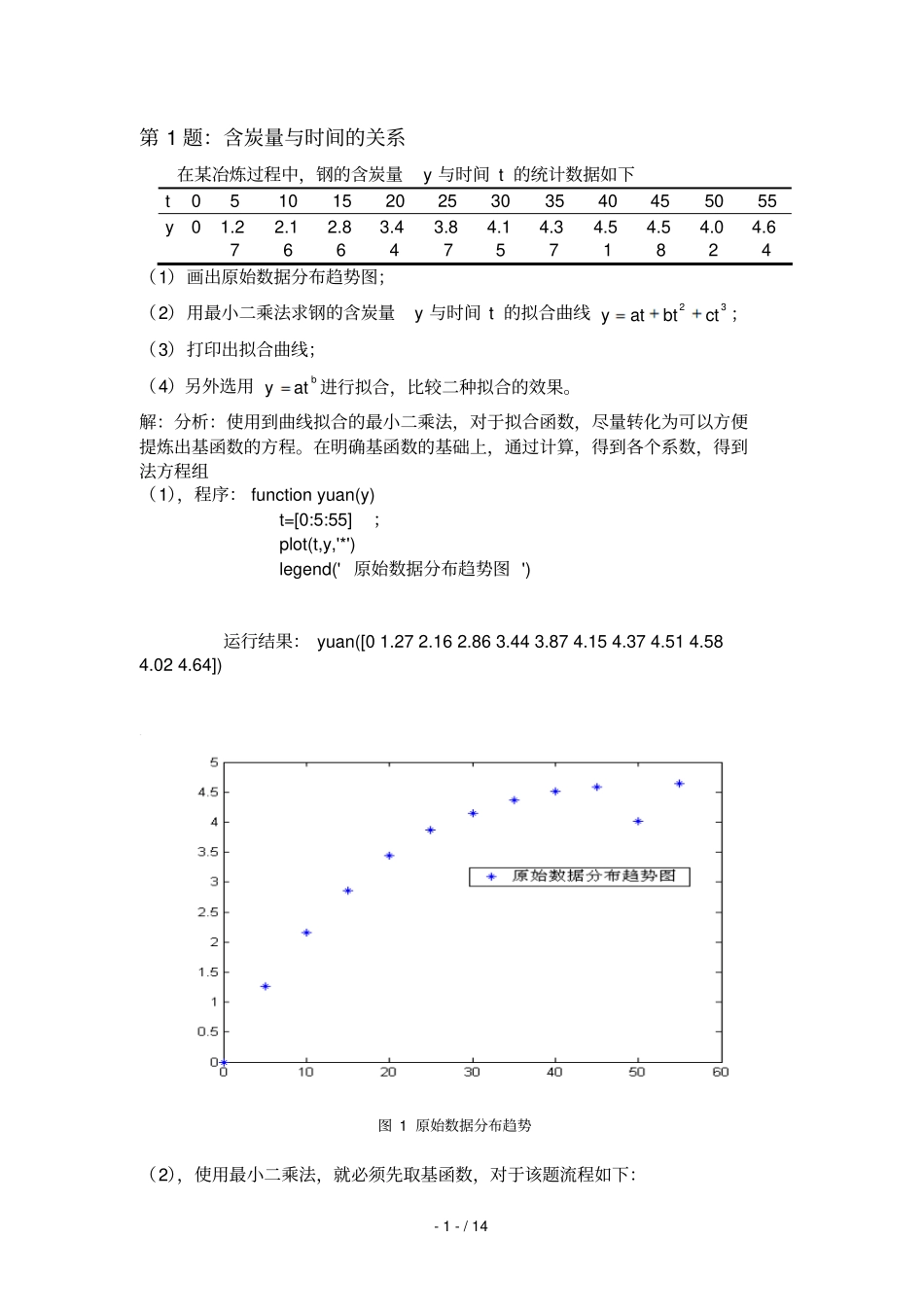
《数值计算方法训练》实习报告题目：6－A 组院系：上海电力学院数理学院专业年级：信息与计算科学专业2009 级学生姓名：XX 远学号：20092426 2011年 7 月 8 日- 1 - / 14 第 1 题：含炭量与时间的关系在某冶炼过程中，钢的含炭量y 与时间 t 的统计数据如下t 0 5 10 15 20 25 30 35 40 45 50 55 y 0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.02 4.64 （1）画出原始数据分布趋势图；（2）用最小二乘法求钢的含炭量y 与时间 t 的拟合曲线32ctbtaty；（3）打印出拟合曲线；（4）另外选用baty进行拟合，比较二种拟合的效果。解：分析：使用到曲线拟合的最小二乘法，对于拟合函数，尽量转化为可以方便提炼出基函数的方程。在明确基函数的基础上，通过计算，得到各个系数，得到法方程组（1），程序： function yuan(y) t=[0:5:55]；plot(t,y,'*') legend(' 原始数据分布趋势图 ') 运行结果： yuan([0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.02 4.64]) 图 1 原始数据分布趋势（2），使用最小二乘法，就必须先取基函数，对于该题流程如下：- 2 - / 14 ①：取基函数为：t021t32t②：由基函数和 y 求法方程组的系数：)(),()(),()(),()()(),()()(),()()(),()()(),()()(),()()(),(212121121101210212122221211211121111212102011210100121000iiiiiiiiiiiiiiiiiiiiiiiiiiixyfxyfxyfxxxxxxxxxxxx③：由这些系数，确定法方程组：BXA),(),(),(),(),(),(),(),(),(),(),(),(210222120121110020100fffBA④：解这个法方程组：cbaXBXA，得到拟合函数：32ctbtaty程序： function [a,b,c]=xian(y0) t0=[0:5:55]; k1=t0; k2=t0.*t0; k3=t0.*t0.*t0; A=[sum(k1.*k1) sum(k2.*k1) sum(k3.*k1);sum(k1.*k2) sum(k2.*k2) sum(k3.*k2);sum(k1.*k3) sum(k2.*k3) sum(k3.*k3)]; B=[sum(k1.*y0);sum(k2.*y0);sum(k3.*y0)]; x=pinv(A)*B; a=x(1,1); b=x(2,1); c=x(3,1); t=0:55; y=a.*t+b.*t.^2+c.*t.^3; plot(t,y,'--') hold on plot(t0,y0,'*') - 3 - / 14 legend('y=a*t+b*t^2+c*t^3拟合效果 ','真实值 ') 运行结果： [a,b,c]=xian([0 1.27 2.16 2.86 3.44 3.87 4.15 4.37 4.51 4.58 4.02 4.64]) a = 0.2657 b = -0.0053 c = 3.5168e-005 （3）拟合的图形，即上一题显示的图像图 2 拟合函数32ctbtaty效果（4），用于这...