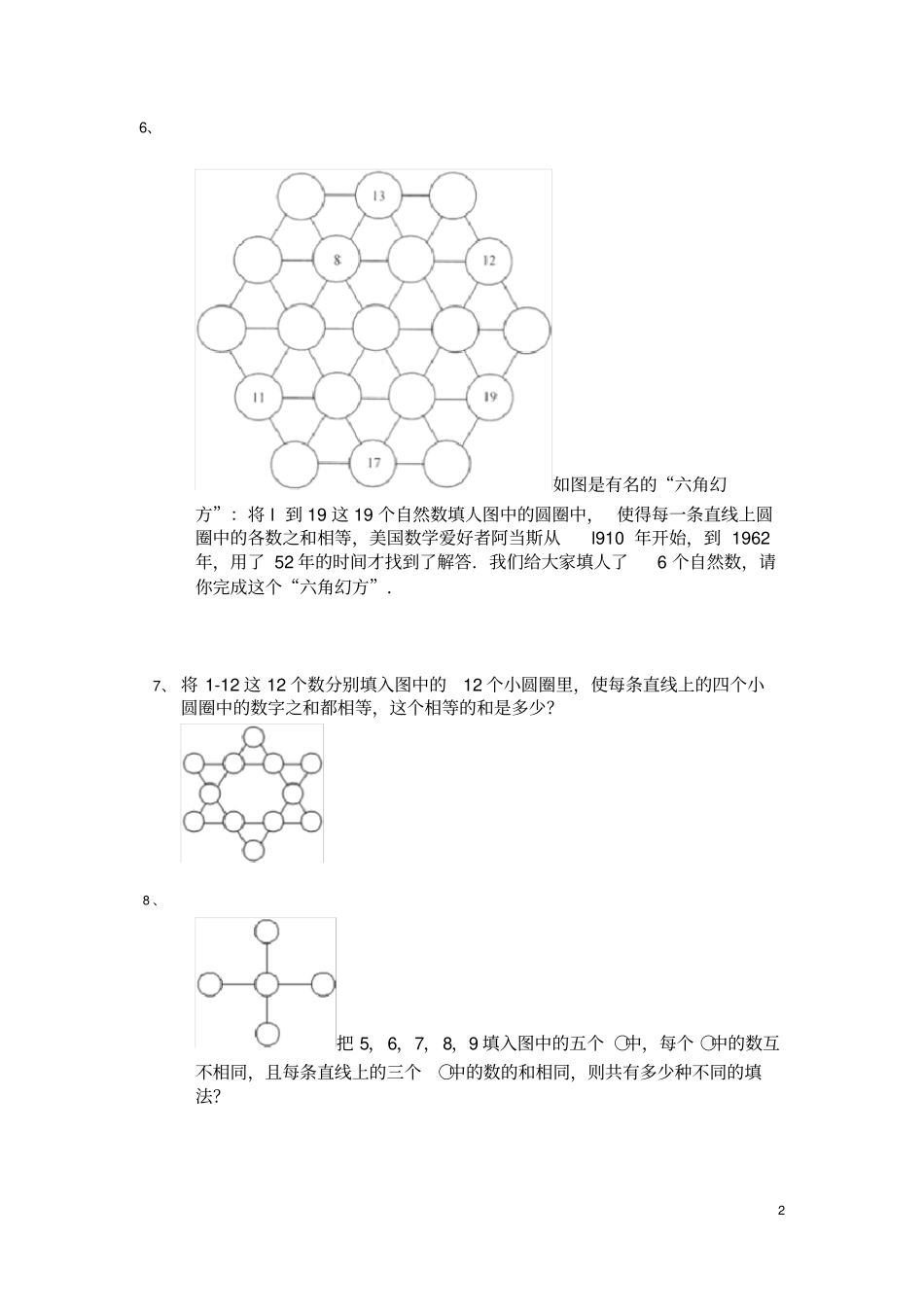
1 2、观察表一寻找规律(表二表三分别是从表一中选取的一部分)。则 a+b=___。表一表二表三3、一列自然数 0,1,2,3 ⋯,2005 ,⋯ ,2024。第一个数是 0,从第二个数开始,每一个都比它前一个大1,最后一个是 2004。现在将这列自然数排成以下数表:⑴第 10 行第 1 个数是?⑵第 1 行第 20 个数是?⑶ 2005 在第几行第几列?4、有一串真分数: 1/2 ,1/3, 2/3, 1/4, 2/4, 3/4,1/5, 2/5 ,3/5, 4/5 ⋯那么第 1001 个分数是___。5、把 5,6,7,8,9 填入图中的五个○中,每个 ○中的数互不相同,且每条直线上的三个○中的数的和相同,则共有多少种不同的填法?数列、数阵练习题1、观察下列各数: 1, 1, 5/7, 7/15, 9/31, ⋯按你发现的规律计算这列数的第7 个数为___。0 1 2 3 ⋯1 3 5 7 ⋯2 5 8 11 ⋯3 7 11 15 ⋯⋯⋯⋯⋯⋯11 14 a 11 13 17 b 0 3 8 15 ⋯1 2 7 14 ⋯4 5 6 13 ⋯9 10 11 12 ⋯⋯⋯⋯⋯⋯2 6、如图是有名的“六角幻方”:将 l 到 19 这 19 个自然数填人图中的圆圈中, 使得每一条直线上圆圈中的各数之和相等,美国数学爱好者阿当斯从l910 年开始,到 1962年,用了 52 年的时间才找到了解答.我们给大家填人了6 个自然数,请你完成这个“六角幻方”.7、 将 1-12 这 12 个数分别填入图中的12 个小圆圈里,使每条直线上的四个小圆圈中的数字之和都相等,这个相等的和是多少? 8 、把 5,6,7,8,9 填入图中的五个 ○中,每个 ○中的数互不相同,且每条直线上的三个○中的数的和相同,则共有多少种不同的填法?3 9、观察下面的数列,找出其中的规律,并根据规律,在括号中填上合适的数 . (1)1,1,2,3,5,8,(),21,34,(2)1,2,2,4,3,8,4,16,5,()(3)2,1,4,3,6,9,8,27,10,(). (4)下面数列的每一项由3 个数组成的数组表示, 它们依次是: (1,3,5),(2,6,10),(3,9,15), 问:第 100 个数组内 3 个数的和是多少?10、先观察算式,找出规律,然后填数。(11-2)÷9=1 (111-3)÷9=12 (1111-4)÷9=123 (11111-)÷9=1234 ( -)÷9=123456 11、找规律填上合适的数。13 20 7 9 17 8 5 9 12、根据数与数的规律, 找出与其他 3 个圆内数的排列规律不同的一个圆。⑴⑵⑶⑷( ) 24 7 5 36 12 6 14 16 7 42 49 6 5 28 35 4 21 2 3...