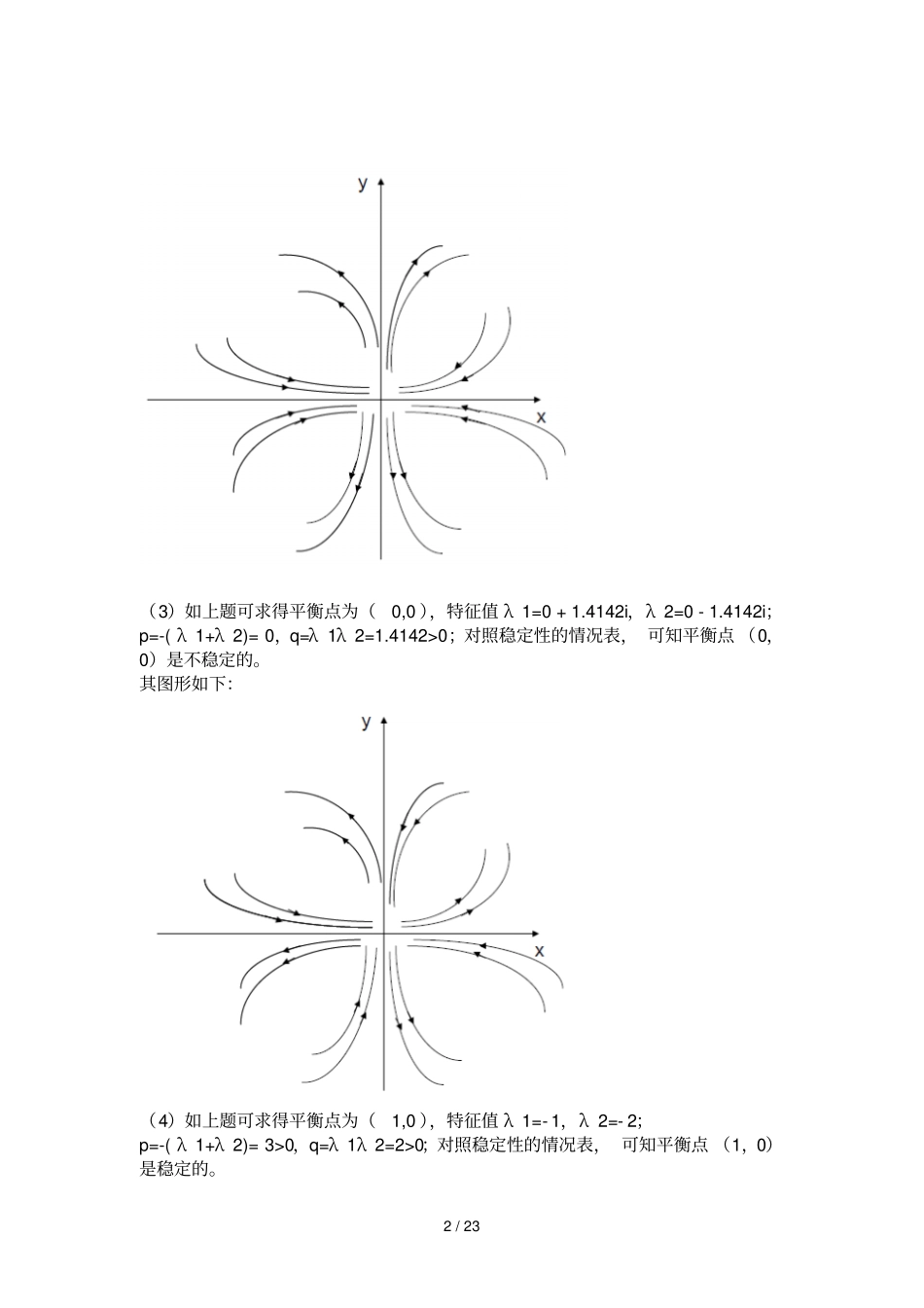
1 / 23 2 微分方程实验1、微分方程稳定性分析根据微分方程稳定性理论, 确定下列资质系统的平衡点, 并说明那些点是稳定的,哪 些 点 是 不 稳 定 , 绘 出 相 应 的 轨 线 , 标 出 随t 郑 家 的 运 动 方 向 。,,,+1,(1)(2)(3)(4);2 ;2 ;2 .dxdxdxdxxxyxdtdtdtdtdydydydyyyxydtdtdtdt解:(1)由 f(x)=x=0,f(y)=y=0;可得平衡点为( 0,0),系数矩阵1001A,求得特征值 λ 1=1,λ 2=1;p=-( λ 1+λ 2)=-2<0 ,q=λ 1λ 2=1>0;对照稳定性的情况表, 可知平衡点 (0,0)是不稳定的。图形如下:(2)如上题可求得平衡点为(0,0 ),特征值 λ 1=- 1,λ 2=2;p=-( λ 1+λ 2)=-1<0 ,q=λ 1λ 2=-2<0;对照稳定性的情况表, 可知平衡点(0,0)是不稳定的。其图形如下:2 / 23 (3)如上题可求得平衡点为(0,0 ),特征值 λ 1=0 + 1.4142i,λ 2=0 - 1.4142i;p=-( λ 1+λ 2)= 0,q=λ 1λ 2=1.4142>0;对照稳定性的情况表, 可知平衡点 (0,0)是不稳定的。其图形如下:(4)如上题可求得平衡点为(1,0 ),特征值 λ 1=- 1,λ 2=- 2;p=-( λ 1+λ 2)= 3>0,q=λ 1λ 2=2>0;对照稳定性的情况表, 可知平衡点 (1,0)是稳定的。3 / 23 其图形如下:2、种群增长模型一个片子上的一群病菌趋向于繁殖成一个圆菌落. 设病菌的数目为N,单位成员的增长率为 r1 ,则由 Malthus 生长律有1dNrNdt,但是,处于周界表面的那些病菌由于寒冷而受到损伤, 它们死亡的数量与 N1/2 成比例,其比例系数为 r2 ,求 N满足的微分方程 . 不用求解, 图示其解族 . 方程是否有平衡解, 如果有, 是否为稳定的 ? 解:由题意很容易列出N满足的微分方程:1212()dNr Nr Nf Ndt令()f N =0,可求得方程的两个平衡点N1=0,N2=2221/rr进而求得11222121221() ()2d Nrr Nr Nr Ndt令220d Ndt可求得 N=2221/ 4rr则 N=N1,N=N2,N=2221/ 4rr 可以把第一象限划为三部分,且从下到上三部分中分别有0,dNdt220,d Ndt;0,dNdt220d Ndt;0,dNdt220d Ndt。4 / 23 则可以画出 N(t )的图形,即微分方程的解族,如下图所示:由图形也可以看出,对于方程的两个平衡点,其中N1=0 是不稳定的; N2=2221/rr 是稳定的。3、有限资源竞争模型1926 年 Volterra提出了两个物种为共同的、有限的食物来源而竞争的模型5 / 23 111112212...