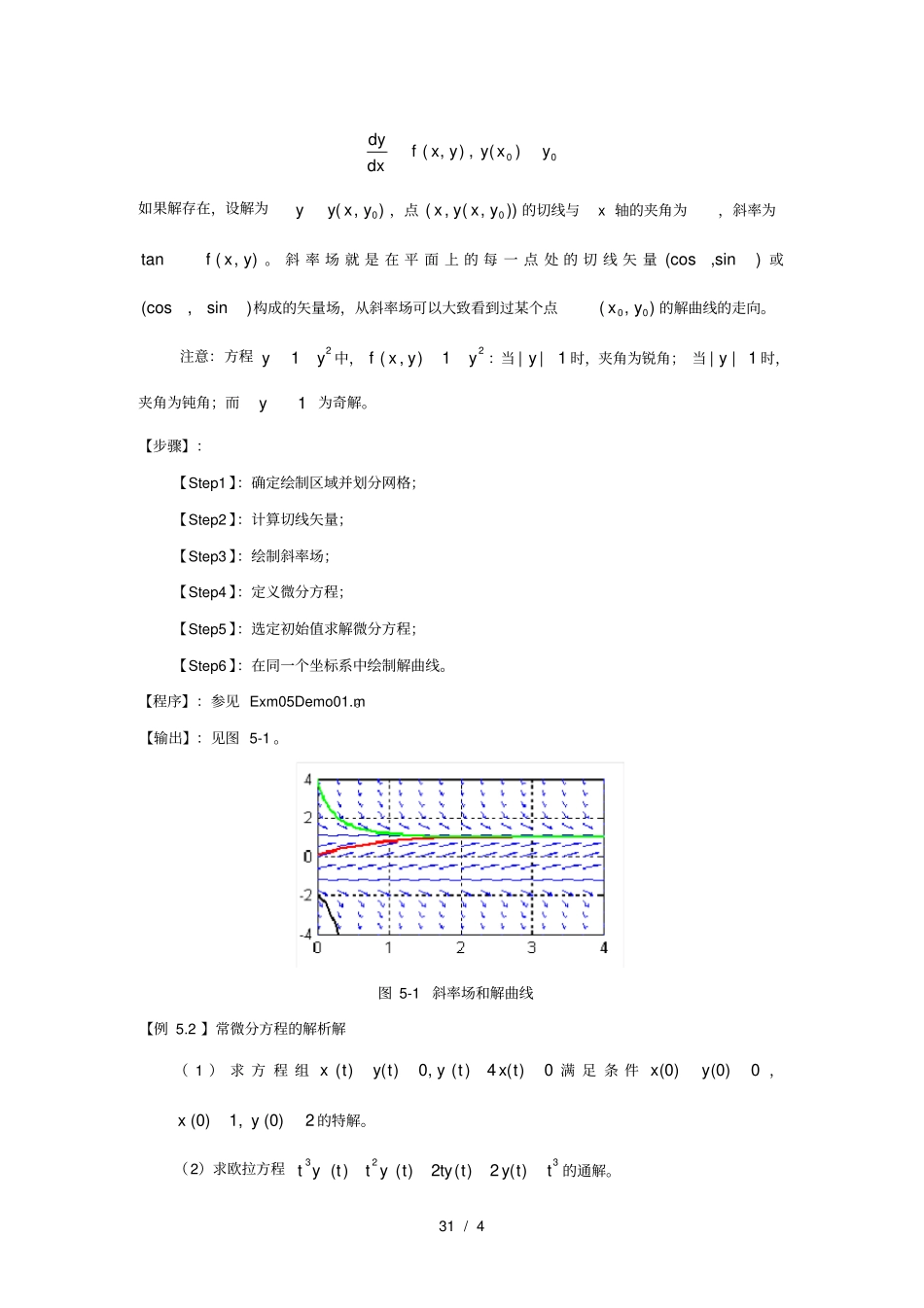
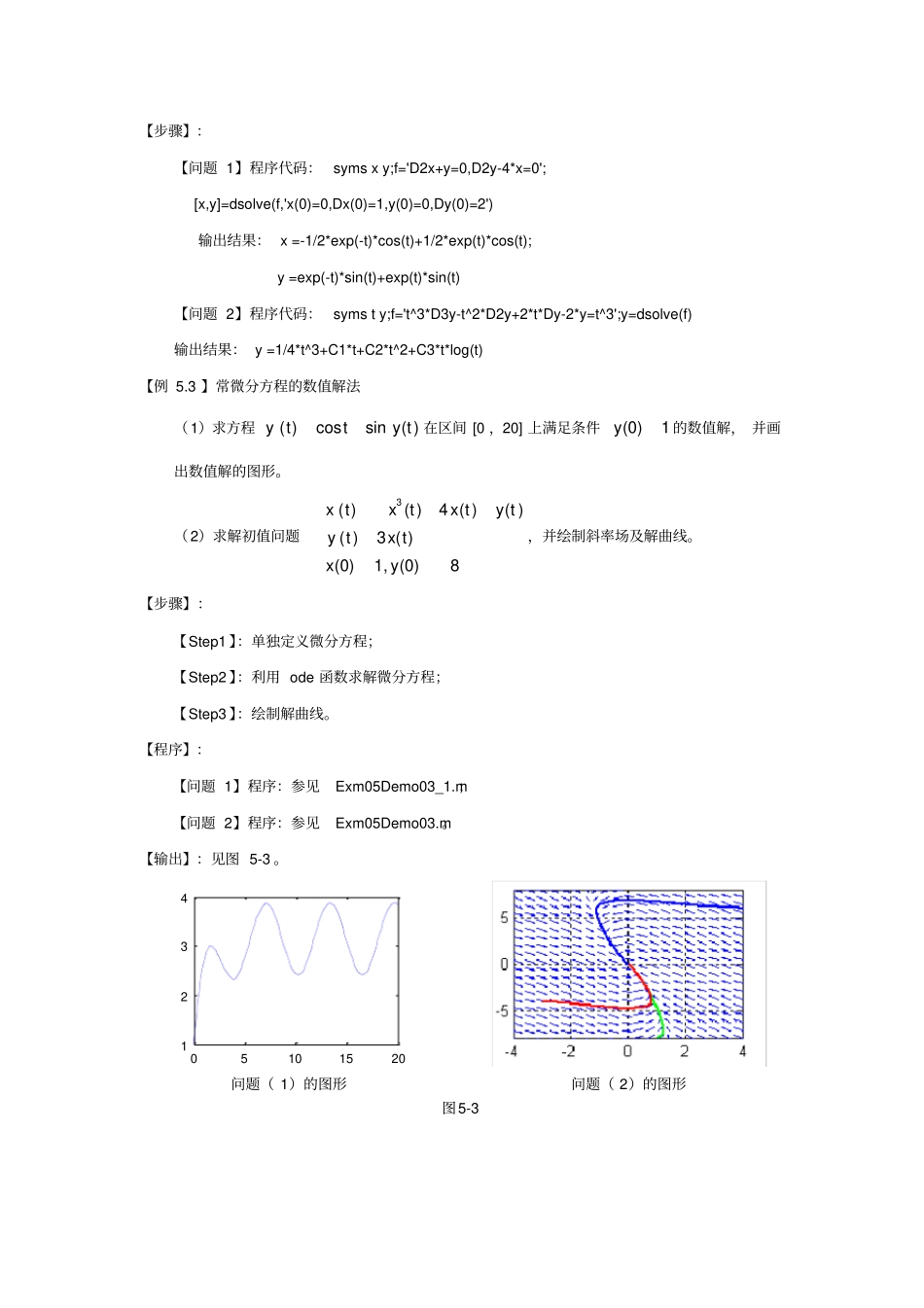
实验 5 微分方程实验目的1.理解方向场、积分曲线的含义2.掌握利用软件求解微分方程的解析解的方法3.掌握利用软件求微分方程数值解的方法4.了解一种微分方程解的稳定性分析方法实验准备1.微分方程、方向场、积分曲线的定义2.复习一阶微分方程的解法3.复习常系数线性微分方程的解法4.自学常微分方程的数值解法实验内容1.常微分方程的方向场与解曲线2.常微分方程的解析解法3.常微分方程的数值解法软件命令表 5-1 Matlab常微分方程命令函数名称调用格式说明syms syms 变量名 1,变量名 2, ⋯定义符号变量sym sym('x',⋯) 定义符号变量dsolve dsolve('常微分方程表达式') 求通解dsolve dsolve('常微分方程表达式','初始条件 ') 求特解ode ode23,ode45 数值解quiver quiver(X0,Y0,X1,Y1,⋯) 绘制向量实验示例【例 5.1 】微分方程的斜率场和积分曲线画出方程21yy 的斜率场,以及积分曲线;【原理】:对一阶微分方程31 / 4 00( ,) ,()dyfx yy xydx如果解存在,设解为0( ,)yy x y,点0(, ( ,))x y x y的切线与x 轴的夹角为,斜率为tan( ,)fx y。 斜 率 场 就 是 在 平 面 上 的 每 一 点 处 的 切 线 矢 量 (cos,sin) 或(cos,sin)构成的矢量场,从斜率场可以大致看到过某个点00(,)xy的解曲线的走向。注意:方程21yy 中,2(,)1fx yy :当 ||1y时,夹角为锐角; 当 || 1y时,夹角为钝角;而1y为奇解。【步骤】:【Step1 】:确定绘制区域并划分网格;【Step2 】:计算切线矢量;【Step3 】:绘制斜率场;【Step4 】:定义微分方程;【Step5 】:选定初始值求解微分方程;【Step6 】:在同一个坐标系中绘制解曲线。【程序】:参见 Exm05Demo01.m。【输出】:见图 5-1 。图 5-1 斜率场和解曲线【例 5.2 】常微分方程的解析解( 1 ) 求 方 程 组( )( )0,( )4 ( )0xty ty tx t满 足 条 件(0)(0)0xy,(0)1,(0)2xy的特解。(2)求欧拉方程323( )( )2( )2 ( )t ytt ytty ty tt 的通解。【步骤】:【问题 1】程序代码: syms x y;f='D2x+y=0,D2y-4*x=0'; [x,y]=dsolve(f,'x(0)=0,Dx(0)=1,y(0)=0,Dy(0)=2') 输出结果: x =-1/2*exp(-t)*cos(t)+1/2*exp(t)*cos(t); y =exp(-t)*sin(t)+exp(t)*sin(t)【问题 2】程序代码: syms t y;f='t^3*D3y-t^2*D2y+2*t*Dy-2*y=t^3';y=dsolve(f)输出结果: y =1/4*t^3+C1*t+C2*t^2+C3*t*l...