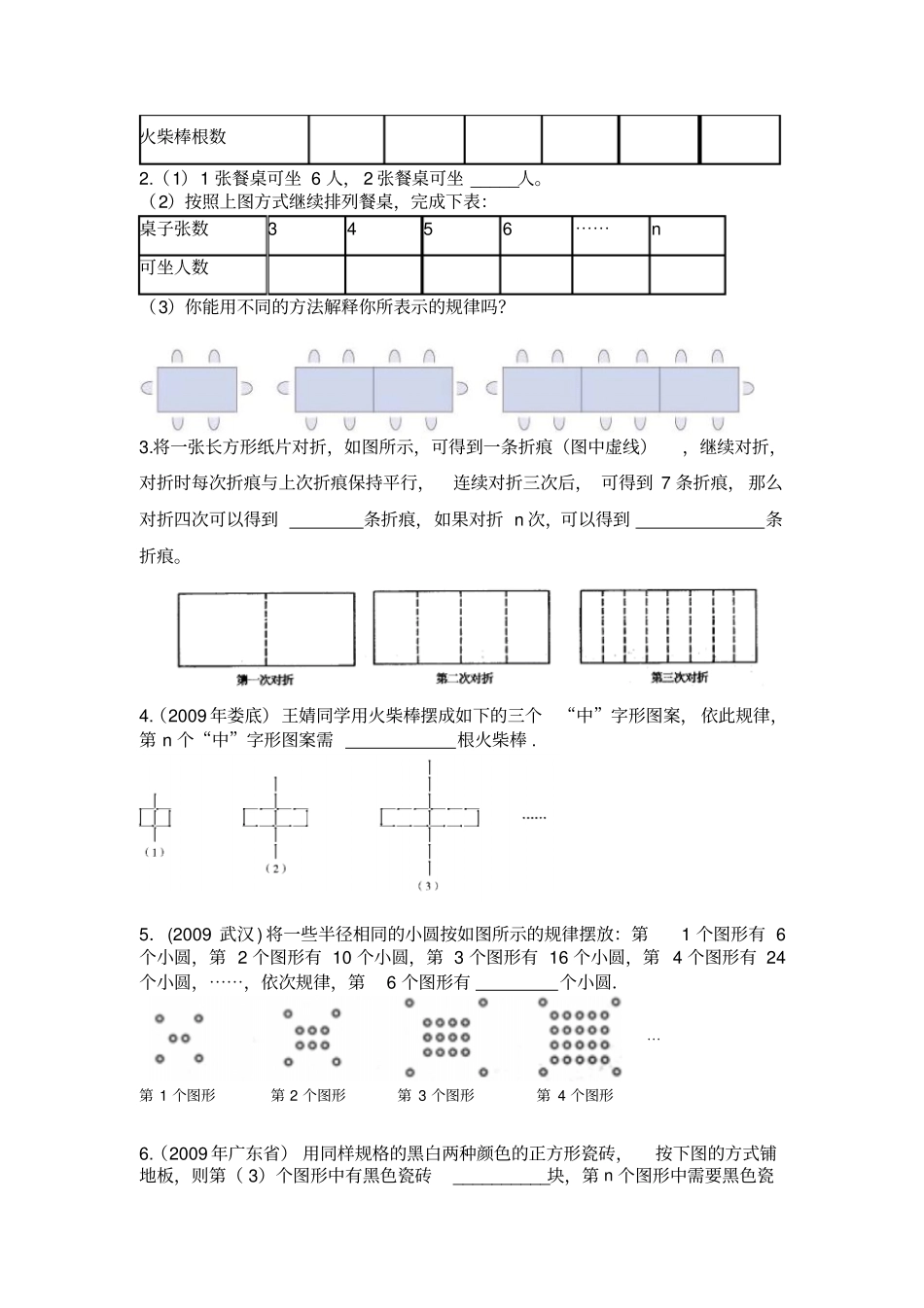
整式的加减、探索规律一、基本知识1.整式的加减即是去括号合并同类项。2.规律题分为图形规律题与式子规律题,找规律时逐一分解。二、正式加减题型(一)化简:1.22aa;yxyx9652. 222213344a bababa b222213;324aabaabb3. ③)(2)(2babaa323712ppppp4.)32(3)23(4)(5bababa)32(2[)3(1yzxxxy] ④2246(23)2xxxx(二)变式题1. 已知22222,3AaabbBaabb ,求: 23AB2.已知222222324,cbaBcbaA,且 A+B+C=0,求多项式 C。3. 化简求值 :222234,1,1x yxyx yxyx yxy其中4. 已知0522baa,求ababaabbaba22224223的值.5,1,232(4)(322 )abababababababba5. 已知求()的值;6.若关于 x 的多项式531225-223nxxxmxx不含二次项和一次项, 求 m,n 的值,并求当 x=-2 时,多项式的值。17、已知实数ba、 与 c 的大小关系如图所示:求cbacba2)(32.三、规律题题型(一)图形题1.用火柴棍拼成一排由三角形组成的图形,如果图形中含有 2,3,或 4 个三角形,分别需要多少根火柴棍?如果图形中含有n 个三角形,需要多少根火柴棍?填写下表三角形个数1 2 3 4 5 n 火柴棒根数2.(1)1 张餐桌可坐 6 人, 2 张餐桌可坐 _____人。(2)按照上图方式继续排列餐桌,完成下表:桌子张数3 4 5 6 ⋯⋯n 可坐人数(3)你能用不同的方法解释你所表示的规律吗?3.将一张长方形纸片对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次折痕保持平行,连续对折三次后, 可得到 7 条折痕, 那么对折四次可以得到条折痕,如果对折 n 次,可以得到条折痕。4.(2009 年娄底)王婧同学用火柴棒摆成如下的三个“中”字形图案, 依此规律,第 n 个“中”字形图案需根火柴棒 .5.(2009 武汉 ) 将一些半径相同的小圆按如图所示的规律摆放:第1 个图形有 6个小圆,第 2 个图形有 10 个小圆,第 3 个图形有 16 个小圆,第 4 个图形有 24个小圆,⋯⋯,依次规律,第6 个图形有个小圆.6.(2009 年广东省) 用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第( 3)个图形中有黑色瓷砖__________块,第 n 个图形中需要黑色瓷第 1 个图形第 2 个图形第 3 个图形第 4 个图形⋯砖__________块(用含 n 的代数式表示).(二)式子题1.研究下列算式,你发现了什么规律?用字母表示这个规律。1×5+4=9=3×3; 2×6+4=16=4×4; 3×7+4=25=5×5; 4×8+4=36=6×6;...