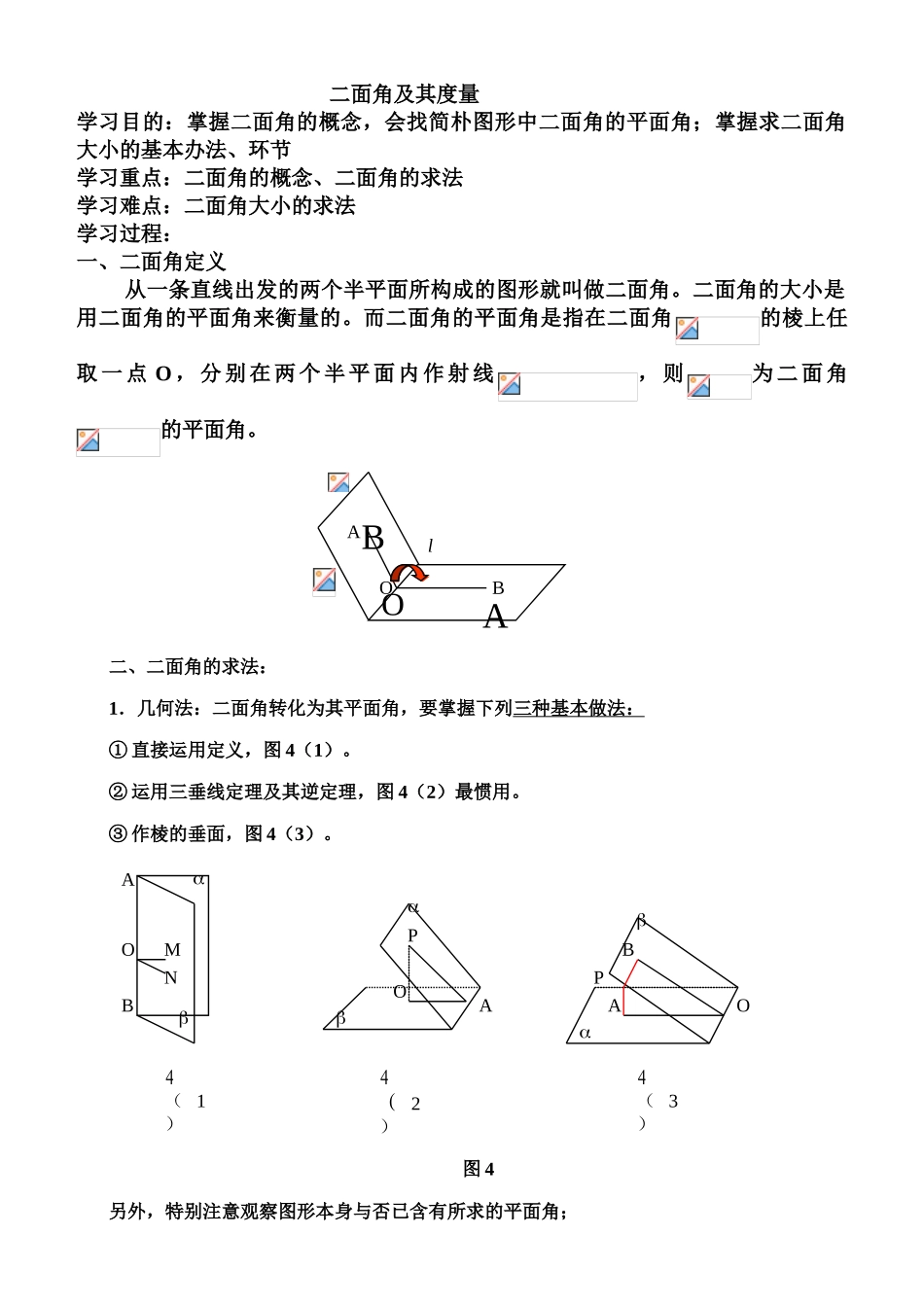
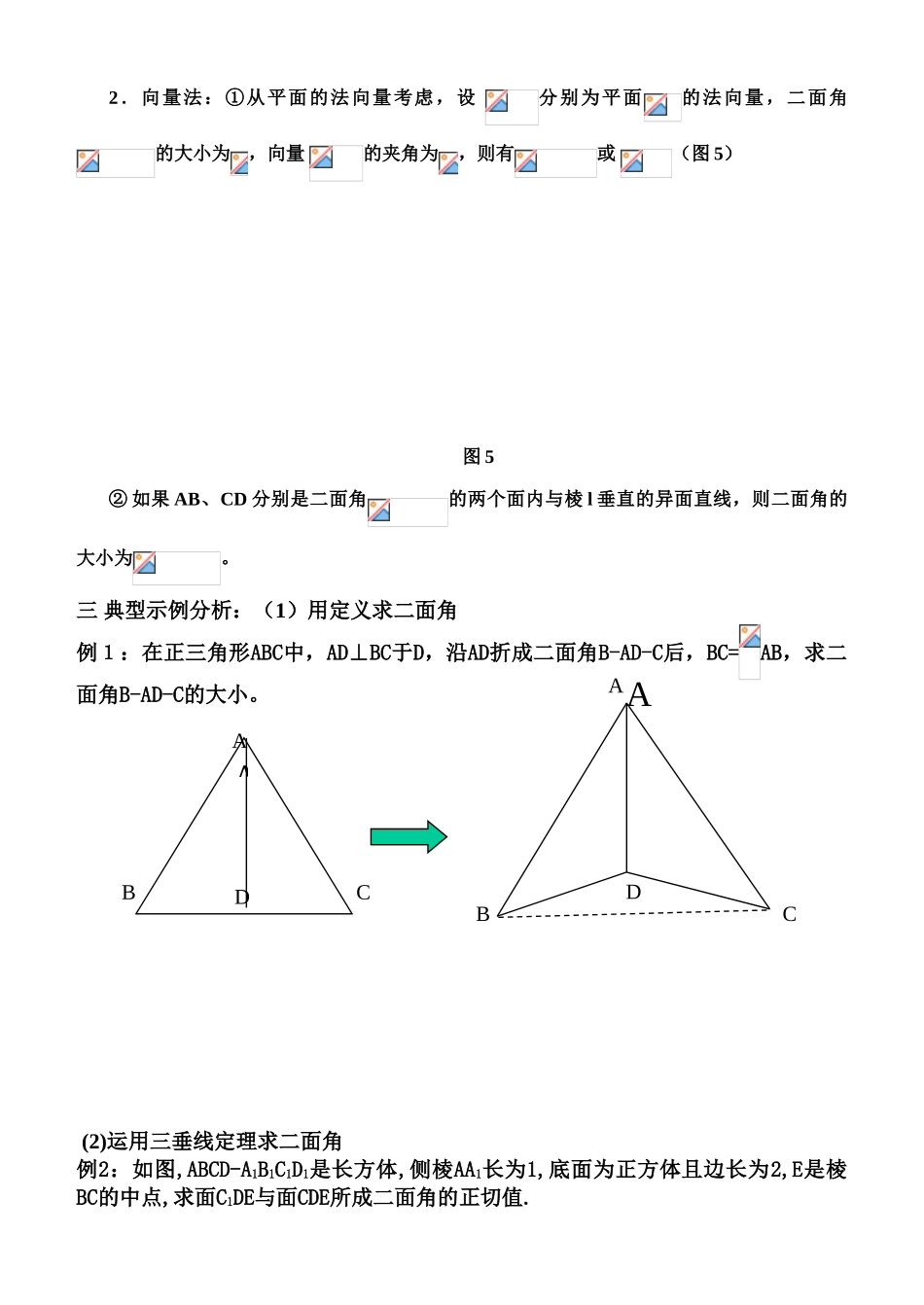
二面角及其度量 学习目的:掌握二面角的概念,会找简朴图形中二面角的平面角;掌握求二面角大小的基本办法、环节学习重点:二面角的概念、二面角的求法学习难点:二面角大小的求法学习过程:一、二面角定义从一条直线出发的两个半平面所构成的图形就叫做二面角。二面角的大小是用二面角的平面角来衡量的。而二面角的平面角是指在二面角的棱上任取 一 点 O , 分 别 在 两 个 半 平 面 内 作 射 线, 则为 二 面 角的平面角。 二、二面角的求法:1.几何法:二面角转化为其平面角,要掌握下列三种基本做法:① 直接运用定义,图 4(1)。② 运用三垂线定理及其逆定理,图 4(2)最惯用。③ 作棱的垂面,图 4(3)。图 4另外,特别注意观察图形本身与否已含有所求的平面角;AOBMNAOPABOP4( 1)4( 2)4( 3)OABOABl2.向量法:①从平面的法向量考虑,设 分别为平面的法向量,二面角的大小为,向量 的夹角为,则有或 (图 5)图 5② 如果 AB、CD 分别是二面角的两个面内与棱 l 垂直的异面直线,则二面角的大小为。三 典型示例分析:(1)用定义求二面角例1:在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=AB,求二面角B-AD-C的大小。 (2)运用三垂线定理求二面角例2:如图,ABCD-A1B1C1D1是长方体,侧棱AA1长为1,底面为正方体且边长为2,E是棱BC的中点,求面C1DE与面CDE所成二面角的正切值.ABCDAABCDA思考:能否用面积摄影法来求?(3)运用空间向量求二面角例 3 : 已 知 四 棱 锥 P-ABCD 的 底 面 为 直 角 梯 形 ,AB∥DC,底面ABCD,且PA=AD=DC=AB=1,M 是 PB 的中点。(Ⅰ)证明:面 PAD⊥面 PCD;(Ⅱ)求 AC 与 PB 所成的角;(Ⅲ)求面 AMC 与面 BMC 所成二面角的大小。二面角的应用例:已知在一种 60°的二面角的棱上有两个点 A、B,AC、BD 分别是在这个二面角的两个面内,且垂直于 AB 的线段,又知 AB=4cm,AC=6cm,BD=8cm,求 CD 的长。 ABCDA1B1C1D1EO变式:⑴如图二面角 α-l-β 中,CA⊥l 于 A,BD⊥l 于 B,又知 AB=4cm,AC=6cm,BD=8cm,CD=,求二面角 α-l-β 的大小。⑵ 如图在 60°的二面角 α-l-β 中 CA⊥l 于 A,BD⊥l 于 B,又知 AC=6cm,BD=8cm,CD=,求 CD 在棱 l 上的射影 AB 的长。达标检测:1、如图,在长方体 ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点 E 在棱 AD 上移动. (1)证明:D1E⊥A1D; (2)当 E 为 AB 的中点时,求点 E 到面 ACD1的距离; (3)AE 等于何值时,二面角 D1—EC—D 的大小为.2、在四棱锥 V-ABCD 中,底面 ABCD 是正方形,侧面 VAD 是正三角形,平面 VAD⊥底面 ABCD.(Ⅰ)证明 AB⊥平面 VAD.(Ⅱ)求面 VAD 与面 VDB 所成的二面角