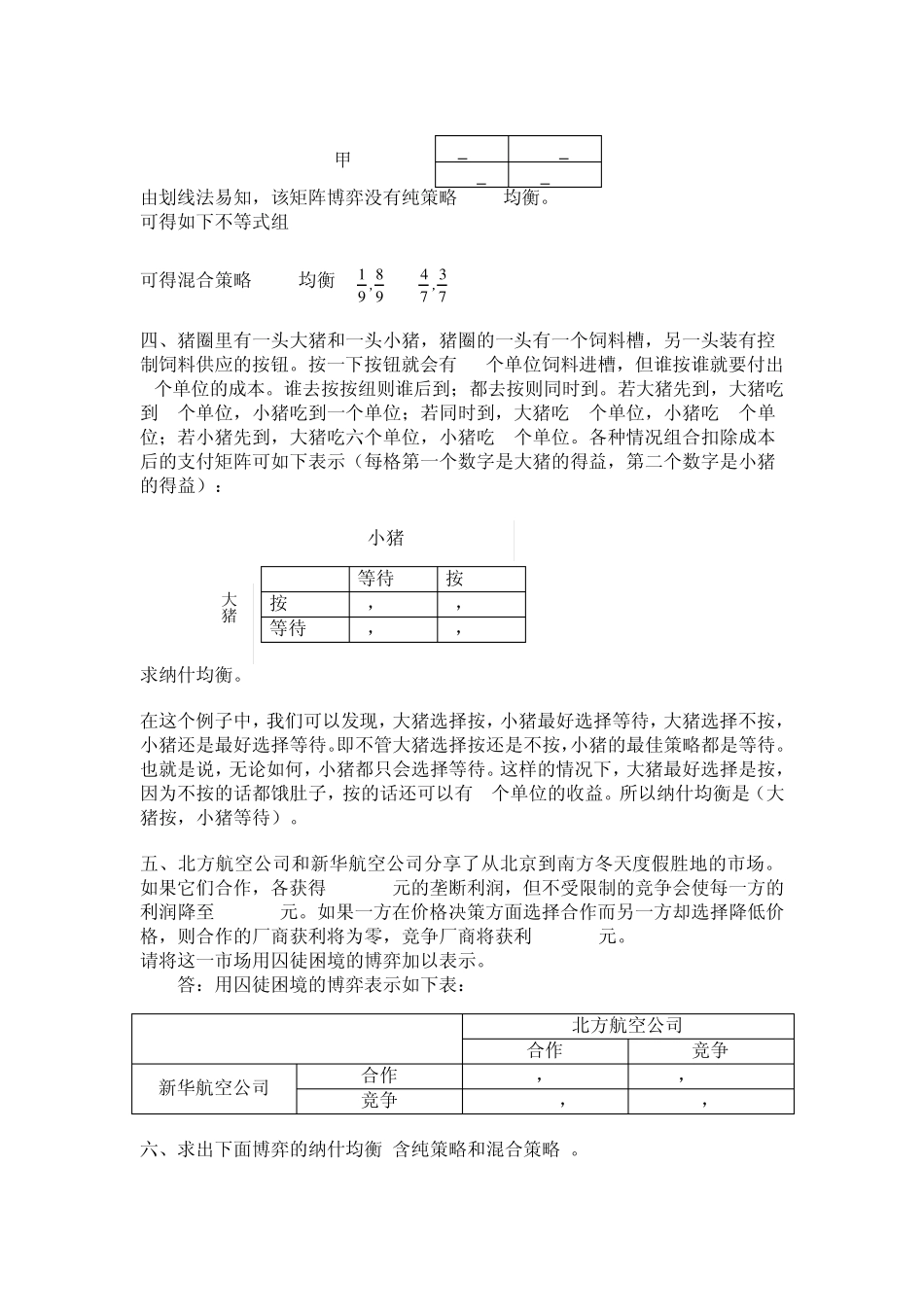
经济博弈论,计算题,全总结,共十题 一、用反应函数法求出下列博弈的所有纯战略纳什均衡。 参与人 2 a b c d A 2,3 3,2 3,4 0,3 参与人1 B 4,4 5,2 0,1 1,2 C 3,1 4,1 1,4 10,2 D 3,1 4,1 -1,2 10,1 解答:纯策略纳什均衡为(B,a)与(A,c) 分析过程:设两个参与人的行动分别为12aa和, player1的反应函数221222,,(),BaaBabR aAacCad 如果如果如果或者D,如果 player2的反应函数112111,,(),DcaAaaBR acaCca 如果如果如果,如果 交点为(B,a)与(A,c),因此纯策略纳什均衡为(B,a)与(A,c)。 二、设啤酒市场上有两家厂商,各自选择是生产高价啤酒还是低价啤酒,相应的利润(单位:万元)由下图的得益矩阵给出: (1)有哪些结果是纳什均衡? (2)两厂商合作的结果是什么? 答(1)(低价,高价),(高价,低价) (2)(低价,高价) 三、求出下面博弈的纳什均衡(含纯策略和混合策略)。 乙 L R 甲 U 5,0 0,8 D 2,6 4,5 由划线法易知,该矩阵博弈没有纯策略Nash均衡。 可得如下不等式组 Q=a+d-b-c=7,q=d-b=4,R=0+5-8-6=-9,r=-1 可得混合策略Nash均衡((9891 , ),(7374 ,) 四、猪圈里有一头大猪和一头小猪,猪圈的一头有一个饲料槽,另一头装有控制饲料供应的按钮。按一下按钮就会有10个单位饲料进槽,但谁按谁就要付出2个单位的成本。谁去按按纽则谁后到;都去按则同时到。若大猪先到,大猪吃到 9个单位,小猪吃到一个单位;若同时到,大猪吃 7个单位,小猪吃 3个单位;若小猪先到,大猪吃六个单位,小猪吃 4个单位。各种情况组合扣除成本后的支付矩阵可如下表示(每格第一个数字是大猪的得益,第二个数字是小猪的得益): 等待 按 按 5,1 4,4 等待 9,-1 0,0 求纳什均衡。 在这个例子中,我们可以发现,大猪选择按,小猪最好选择等待,大猪选择不按,小猪还是最好选择等待。即不管大猪选择按还是不按,小猪的最佳策略都是等待。也就是说,无论如何,小猪都只会选择等待。这样的情况下,大猪最好选择是按,因为不按的话都饿肚子,按的话还可以有4个单位的收益。所以纳什均衡是(大猪按,小猪等待)。 五、北方航空公司和新华航空公司分享了从北京到南方冬天度假胜地的市场。如果它们合作,各获得500000元的垄断利润,但不受限制的竞争会使每一方的利润降至 60000元。如果一方在价格决策方面选择合作而...