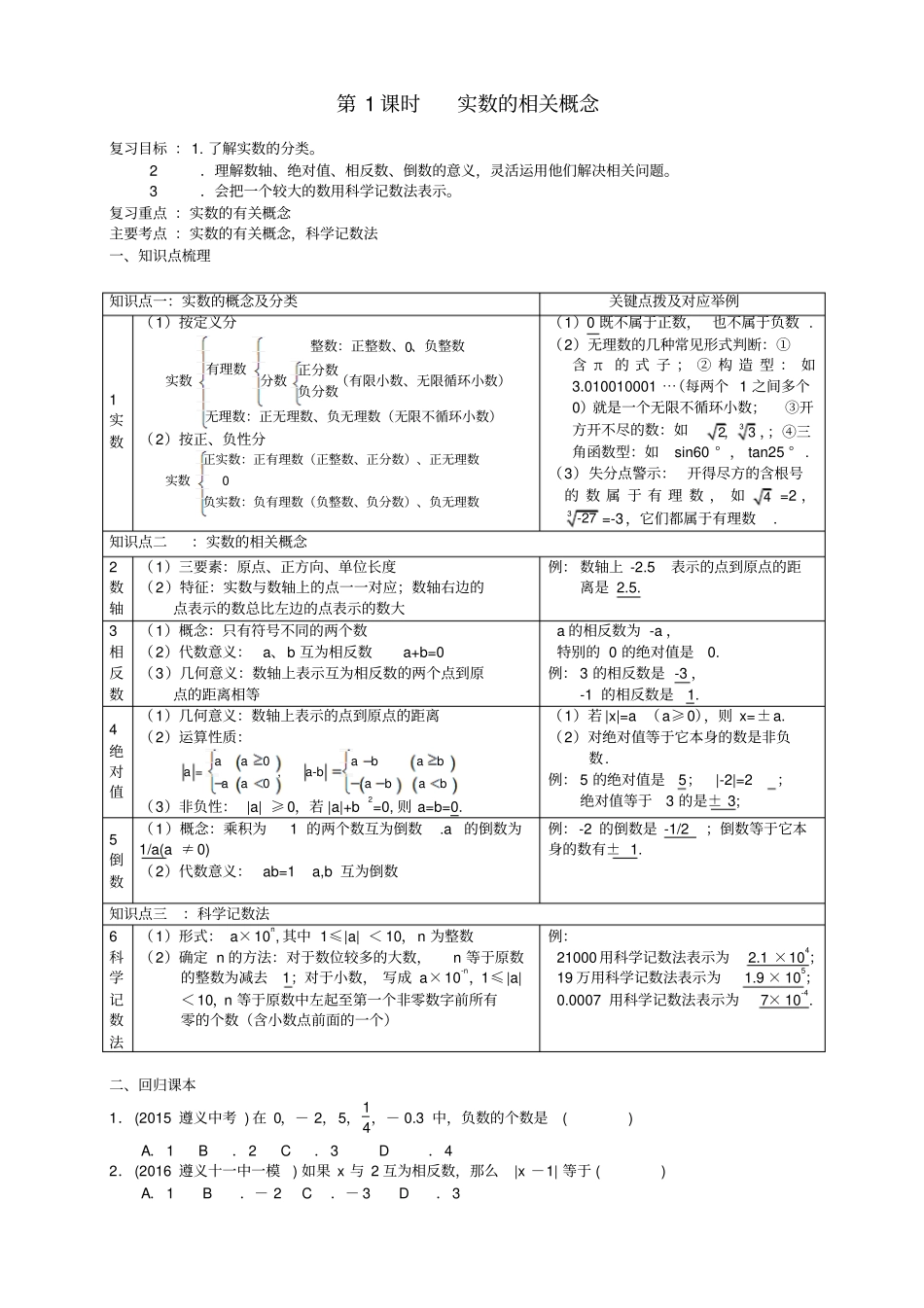
第 1 课时实数的相关概念复习目标 :1. 了解实数的分类。 2.理解数轴、绝对值、相反数、倒数的意义,灵活运用他们解决相关问题。 3.会把一个较大的数用科学记数法表示。复习重点 :实数的有关概念主要考点 :实数的有关概念,科学记数法一、知识点梳理二、回归课本1.(2015 遵义中考 ) 在 0,- 2,5,14,- 0.3 中,负数的个数是( ) A.1 B.2 C.3 D.4 2.(2016 遵义十一中一模) 如果 x 与 2 互为相反数,那么|x -1| 等于 ( ) A.1 B.- 2 C.- 3 D.3 知识点一:实数的概念及分类关键点拨及对应举例1实数(1)按定义分0整数:正整数、 、负整数有理数正分数实数分数(有限小数、无限循环小数)负分数无理数:正无理数、负无理数(无限不循环小数)(2)按正、负性分正实数:正有理数(正整数、正分数)、正无理数实数0负实数:负有理数(负整数、负分数)、负无理数(1)0 既不属于正数, 也不属于负数 . (2)无理数的几种常见形式判断:①含 π的 式 子 ; ② 构 造 型 : 如3.010010001 ⋯(每两个 1 之间多个0)就是一个无限不循环小数;③开方开不尽的数:如323,,;④三角函数型:如sin60 ° , tan25 ° . (3)失分点警示: 开得尽方的含根号的 数 属 于 有 理 数 , 如4 =2 ,3 -27 =-3,它们都属于有理数. 知识点二:实数的相关概念2数轴(1)三要素:原点、正方向、单位长度(2)特征:实数与数轴上的点一一对应;数轴右边的点表示的数总比左边的点表示的数大例: 数轴上 -2.5表示的点到原点的距离是 2.5.3相反数(1)概念:只有符号不同的两个数(2)代数意义: a、b 互为相反数 a+b=0 (3)几何意义:数轴上表示互为相反数的两个点到原点的距离相等a 的相反数为 -a ,特别的 0 的绝对值是0. 例: 3 的相反数是 -3 ,-1 的相反数是1. 4绝对值(1)几何意义:数轴上表示的点到原点的距离(2)运算性质:0a =,a-b0aaababaaabab(3)非负性: |a| ≥0,若 |a|+b2=0, 则 a=b=0. (1)若 |x|=a (a≥0),则 x=±a. (2)对绝对值等于它本身的数是非负数. 例: 5 的绝对值是5; |-2|=2;绝对值等于3 的是± 3; 5倒数(1)概念:乘积为1 的两个数互为倒数.a的倒数为1/a(a ≠0) (2)代数意义: ab=1a,b 互为倒数例:-2 的倒数是 -1/2 ;倒数等于它本身的数有± 1.知识点三:科学记数法6科学记数法(...