过程装备基础第5章习题解VIP免费

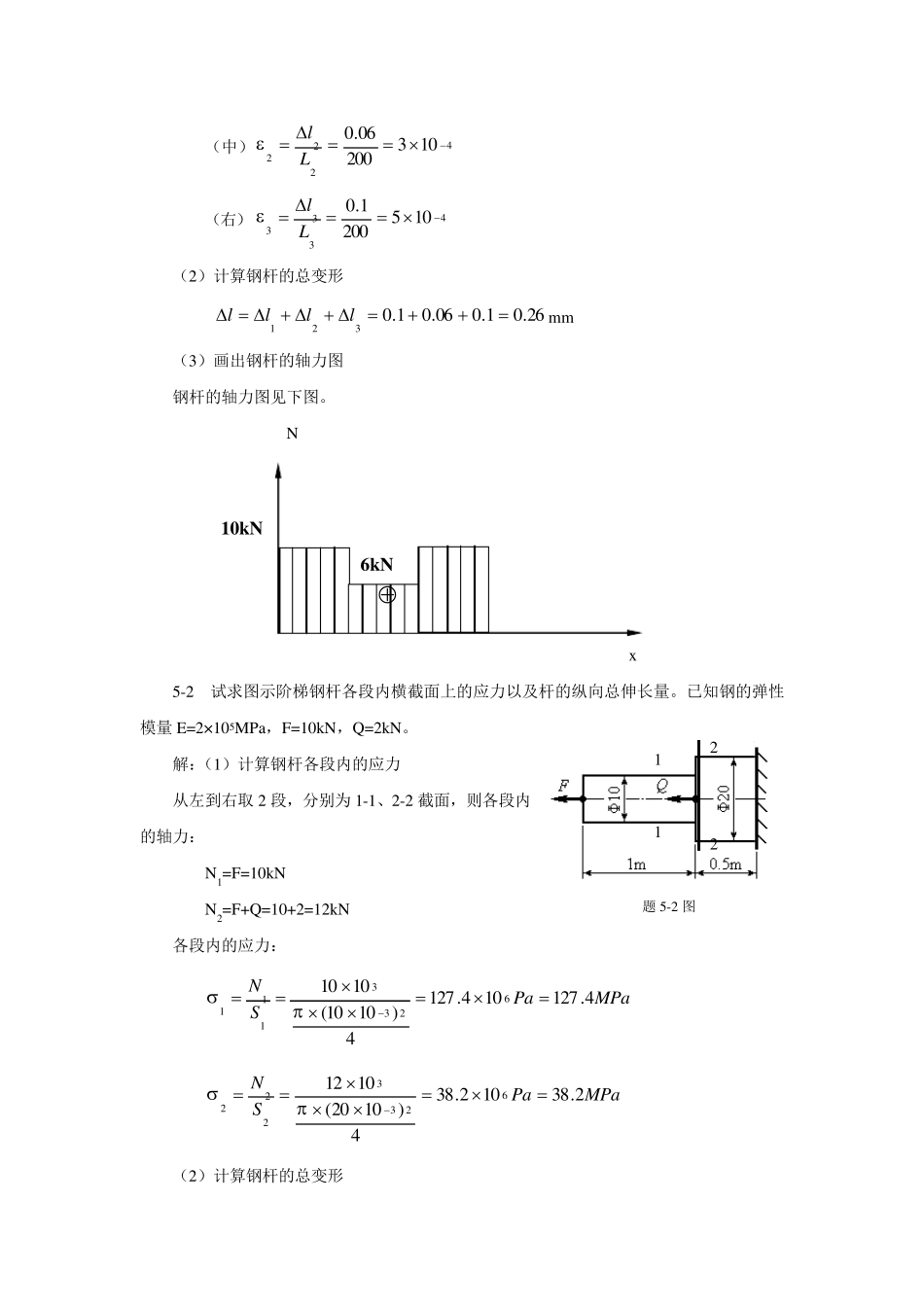
第5 章 杆件的强度与刚度计算 5-1 如图所示的钢杆，已知：杆的横截面面积等于100mm2，钢的弹性模量E=2×105MPa，F=10kN，Q=4kN。要求： （1）计算钢杆各段的应力、绝对变形和应变； （2）计算钢杆的纵向总伸长量。 解：（1）计算钢杆各段内的轴力、应力、绝对变形和应变 从左到右取 3 段，分别为 1-1、2-2、3-3 截面，则根据轴力的平衡，得 各段内的轴力：（左）N1=F=10kN （中）N2=F-Q=10-4=6kN （右）N3=F =10=10kN 各段内的应力： （左）MPaPaSN1001010010100101066311 （中）MPaPaSN6010601010010666322 （右）MPaPaSN1001010010100101066333 各段内的绝对变形： （左）m mmESLNl1.0101.0)10100()102(2.0)1010(3653111 （中） m mmESLNl06.01006.0)10100()102(2.0)106(3653222 （右）m mmESLNl1.0101.0)10100()102(2.0)1010(3653333 各段内的应变： （左）41111052001.0 Ll 题 5-1 图 1 2 3 1 2 3 （中）422210320006.0 Ll （右）43331052001.0 Ll （2）计算钢杆的总变形 26.01.006.01.0321llllmm （3）画出钢杆的轴力图 钢杆的轴力图见下图。 N x 5-2 试求图示阶梯钢杆各段内横截面上的应力以及杆的纵向总伸长量。已知钢的弹性模量E=2×105MPa，F=10kN，Q=2kN。 解：（1）计算钢杆各段内的应力 从左到右取2 段，分别为1-1、2-2 截面，则各段内的轴力： N1=F=10kN N2=F+Q=10+2=12kN 各段内的应力： MPaPaSN4.127104.1274)1010(10106233111 MPaPaSN2.38102.384)1020(10126233222 （2）计算钢杆的总变形  10kN 6kN 题 5-2 图 1 1 2 2 各段的变形： mmmESLNl637.010637.04)1010(10210001010323531111 mmmESLNl096.010096.04)1020(1025001012323531112 故钢杆的总变形： 733.0096.0637.021lllmm 5-3 如图所示的三角形支架，杆AB 和杆BC 均为圆截面，杆AB 的直径d1=20mm，杆BC 的直径d2=40mm，两杆材料的许用应力均为[σ]=160MPa 。设重物的重量 G=20kN，试问此支架是？ 解：（1）取 B 点作为研究对象，画出如图...