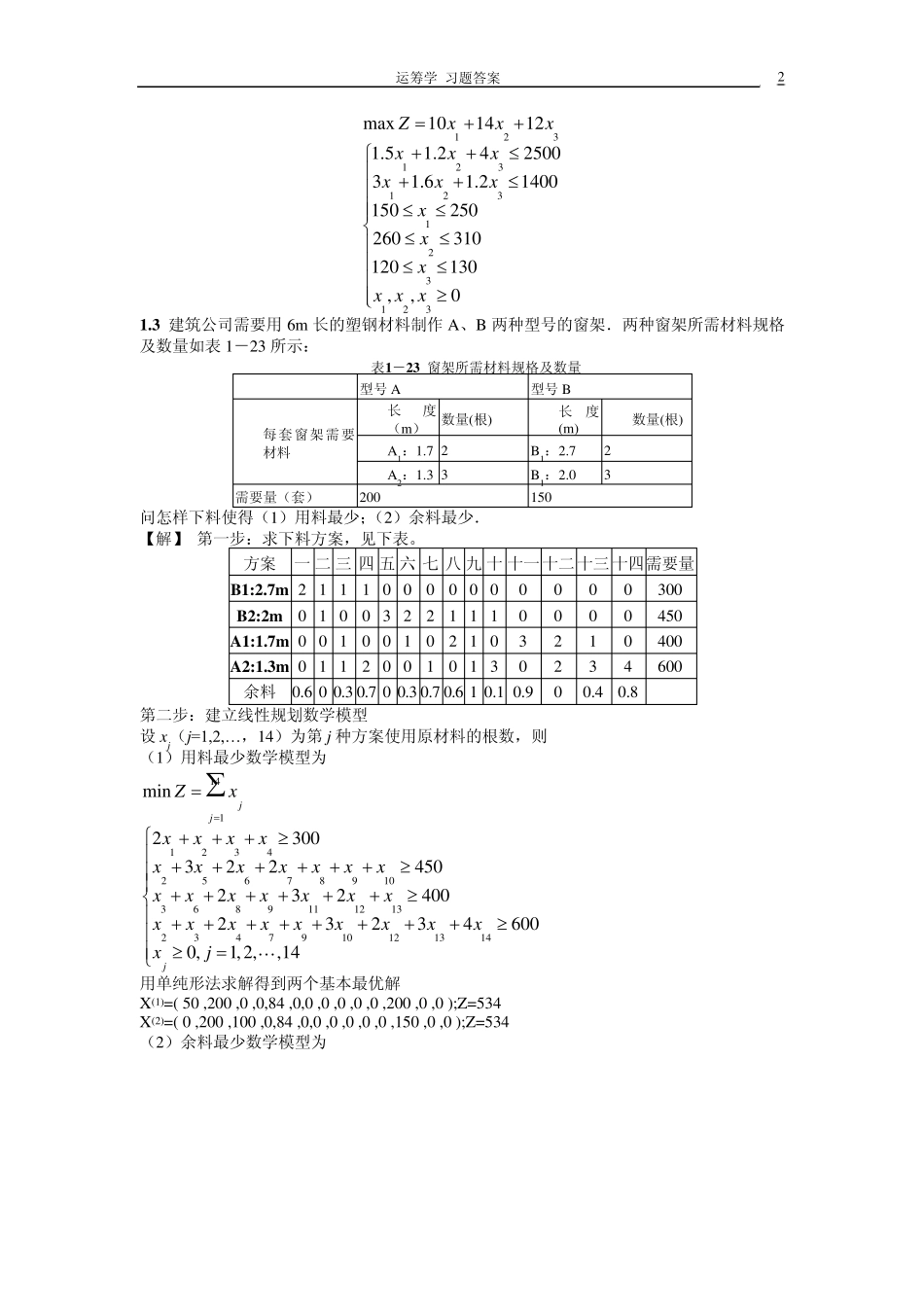
运筹学 习题答案 1 教材习题答案 部分有图形的答案附在各章 PPT 文档的后面,请留意。 第 1 章 线性规划 第 2 章 线性规划的对偶理论 第 3 章 整数规划 第 4 章 目标规划 第 5 章 运输与指派问题 第 6 章 网络模型 第 7 章 网络计划 第 8 章 动态规划 第 9 章 排队论 第 10 章 存储论 第 11 章 决策论 第 12 章 对策论 习题一 1 .1 讨论下列问题: (1)在例 1.1 中,假定企业一周内工作 5 天,每天 8 小时,企业设备 A 有 5 台,利用率为0.8,设备 B 有 7 台,利用率为 0.85,其它条件不变,数学模型怎样变化. (2)在例 1.2 中,如果设 x j(j=1,2,…,7)为工作了 5 天后星期一到星期日开始休息的营业员,该模型如何变化. (3)在例 1.3 中,能否将约束条件改为等式;如果要求余料最少,数学模型如何变化;简述板材下料的思路. (4)在例 1.4 中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化. (5)在例 1.6 中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1 小时,模型如何变化. 1 .2 工厂每月生产A、B、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表 1-22 所示. 表1 -2 2 产品 资源 A B C 资源限量 材料(k g) 1.5 1.2 4 2500 设备(台时) 3 1.6 1.2 1400 利润(元/件) 10 14 12 根据市场需求,预测三种产品最低月需求量分别是 150、260 和 120,最高月需求是 250、310和 130.试建立该问题的数学模型,使每月利润最大. 【解】设 x 1、x 2、x 3 分别为产品 A、B、C 的产量,则数学模型为 运筹学 习题答案 2 123123123123123max1014121.51.24250031.61.21400150250260310120130,,0Zxxxxxxxxxxxxxxx 1.3 建筑公司需要用6m 长的塑钢材料制作A、B 两种型号的窗架.两种窗架所需材料规格及数量如表 1-23 所示: 表1-23 窗架所需材料规格及数量 型号 A 型号 B 每套窗架需要材料 长度(m) 数量(根) 长度(m) 数量(根) A1:1.7 2 B1:2.7 2 A2:1.3 3 B1:2.0 3 需要量(套) 200 150 问怎样下料使得(1)用料最少;(2)余料最少. 【解】 第一步:求下料方案,见下表。 方案 一 二...