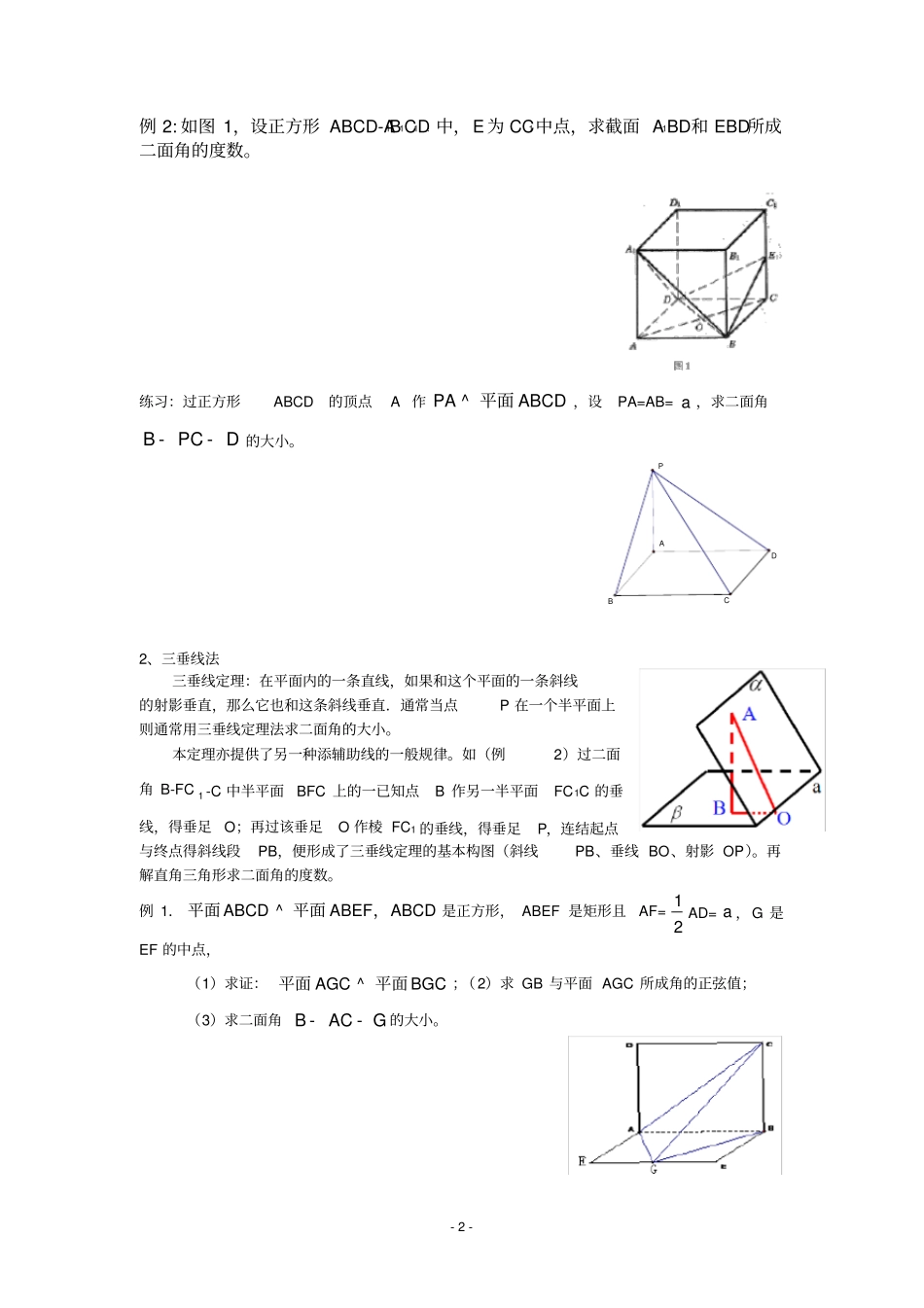
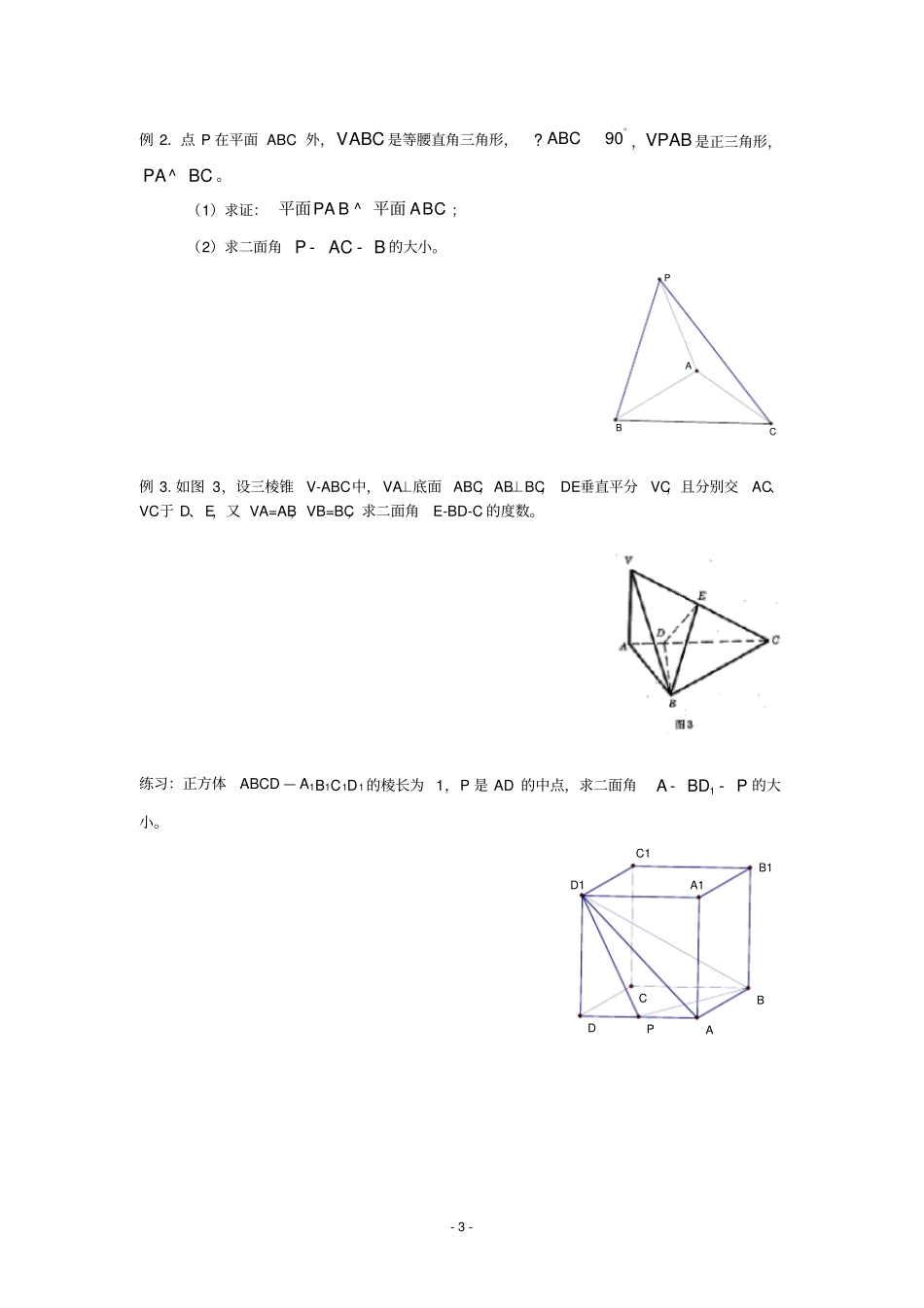
- 1 - aOAB立体几何二面角求法一:知识准备1、二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱 , 这两个半平面叫做二面角的面. 2、二面角的平面角的概念:平面角是指以二面角的棱上一点为端点,在两个半平面内分别做垂直于棱的两条射线,这两条射线所成的角就叫做该二面角的平面角。3、二面角的大小范围:[0° , 180°] 4、三垂线定理 :平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直5、平面的法向量 :直线 L 垂直平面α ,取直线L 的方向向量,则这个方向向量叫做平面α的法向量。(显然,一个平面的法向量有无数个,它们是共线向量)6、二面角做法:做二面角的平面角主要有3 种方法:( 1)、定义法:在棱上取一点,在两个半平面内作垂直于棱的2 条射线,这2 条所夹的角;( 2)、垂面法:做垂直于棱的一个平面,这个平面与2 个半平面分别有一条交线,这2条交线所成的角;( 3)、三垂线法:过一个半平面内一点(记为A )做另一个半平面的一条垂线,过这个垂足(记为 B)再做棱的垂线,记垂足为C,连接 AC,则∠ ACB 即为该二面角的平面角。7、两个平面的法向量的夹角与这两个平面所成的二面角的平面角有怎样的关系?二:二面角的基本求法及练习1、定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。本定义为解题提供了添辅助线的一种规律。如例 1 中从二面角S— AM— B 中半平面 ABM 上的一已知点(B)向棱 AM 作垂线,得垂足(F);在另一半平面ASM 内过该垂足( F)作棱 AM 的垂线(如GF),这两条垂线( BF、GF)便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。例 1.在正方体ABCD — A1B1C1D 1 中,求(1)二面角11AB CA--的大小;(2)平面11A DC 与平面11ADD A 所成角的正切值。C1D1B1A1CDAB- 2 - 例 2: 如图 1,设正方形 ABCD-A1B1C1D!中,E 为 CC1中点,求截面 A1BD和 EBD所成二面角的度数。练习:过正方形ABCD的顶点A 作 PAABCD^ 平面,设PA=AB= a ,求二面角BPCD--的大小。BACDP2、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条...