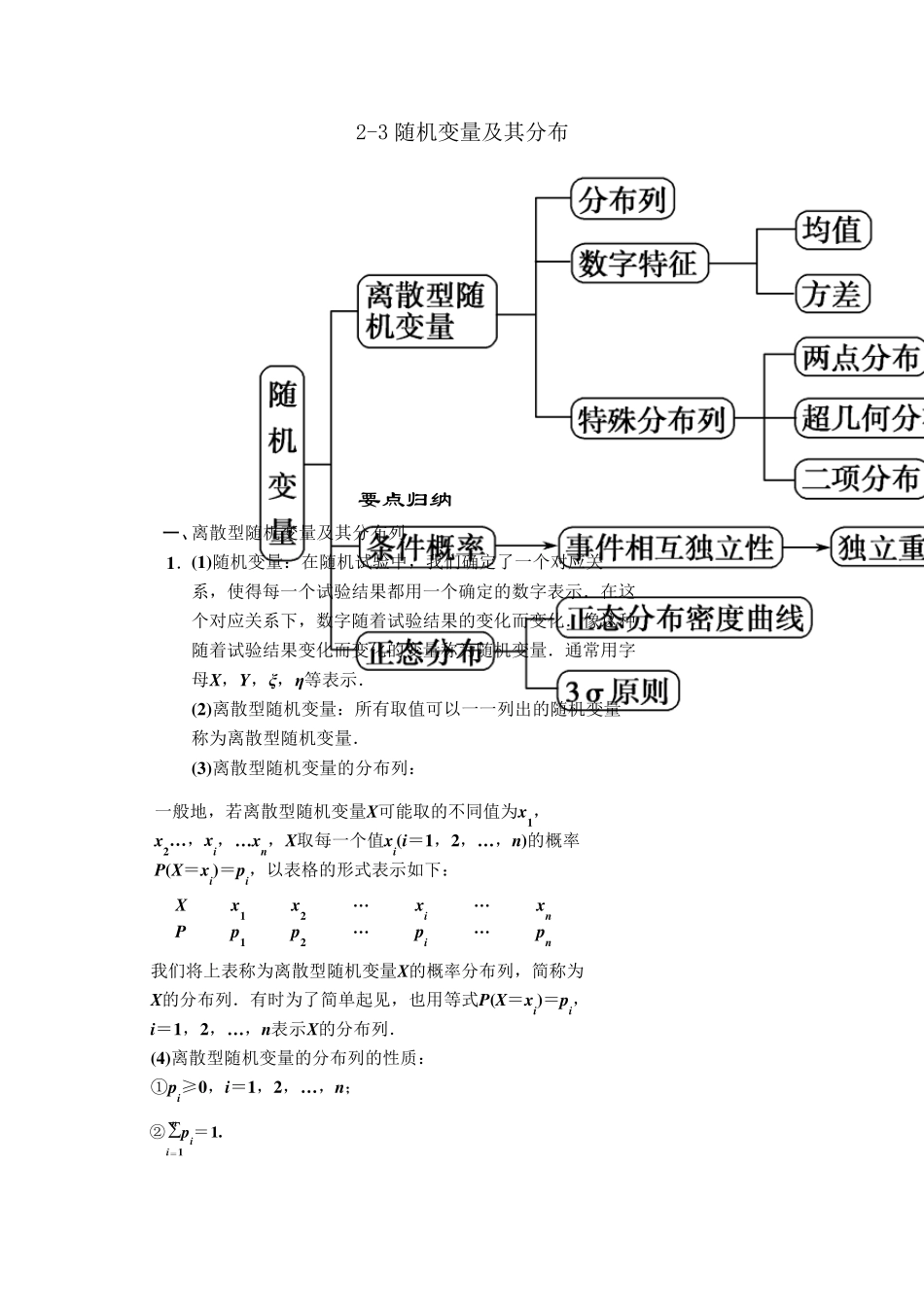
2-3 随机变量及其分布 离散型随机变量及其分布列(1 )随机变量:在随机试验中,我们确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示.在这个对应关系下,数字随着试验结果的变化而变化.像这种随着试验结果变化而变化的变量称为随机变量.通常用字母X,Y,ξ,η等表示.(2 )离散型随机变量:所有取值可以一一列出的随机变量称为离散型随机变量.(3 )离散型随机变量的分布列:要点归纳一、1 . 一般地,若离散型随机变量X可能取的不同值为x1,x2 …,xi,…xn,X取每一个值xi(i=1 ,2 ,…,n)的概率P(X=xi)=pi,以表格的形式表示如下:Xx1x2…xi…xnPp1p2…pi…pn我们将上表称为离散型随机变量X的概率分布列,简称为X的分布列.有时为了简单起见,也用等式P(X=xi)=pi,i=1 ,2 ,…,n表示X的分布列.(4 )离散型随机变量的分布列的性质:①pi≥0 ,i=1 ,2 ,…,n;②i=1n pi=1 . (5)常见的分布列:两点分布:如果随机变量X的分布列具有下表的形式,则称X服从两点分布,并称p=P(X=1)为成功概率.X01P1-pp两点分布又称0-1 分布,伯努利分布. 超几何分布:一般地,在含有M 件次品的N 件产品中,任取n 件,其中恰有X 件次品,则事件{X=k} 发生的概率为P(X=k)=CkMCn-kN-MCnN,k=0,1,2,…,m,即 X01…mP…C0MCn-0N-MCnN C1MCn-1N-MCnN CmMCn-mN-MCnN 其中m=min{M,n} ,且n≤N,M≤N,n,M,N∈N*.如果随机变量X的分布列具有上表的形式,则称随机变量X服从超几何分布.二项分布及其应用2.(1)条件概率:一般地,设 A 和 B 是两个事件,且 P(A)>0,称P(B|A)=P(AB)P(A) 为在事件A 发生的条件下,事件B 发生的条件概率.P(B|A)读作 A 发生的条件下B 发生的概率. (2)条件概率的性质:①0≤P(B|A)≤1;②必然事件的条件概率为1,不可能事件的条件概率为0; (4)独立重复试验:一般地,在相同条件下重复做的n次试验称为n次独立重复试验.(5)二项分布:一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为③如果B 和 C 是两个互斥事件,则P(B∪C|A)=P(B|A)+P(C|A). (3)事件的相互独立性:设 A,B 为两个事件,如果P(AB)=P(A)P(B),则称事件A 与事件B 相互独立.如果事件A 与 B相互独立,那么 A 与 B-,A-与 B,A-与 B-也都相互独立. P(X=k...