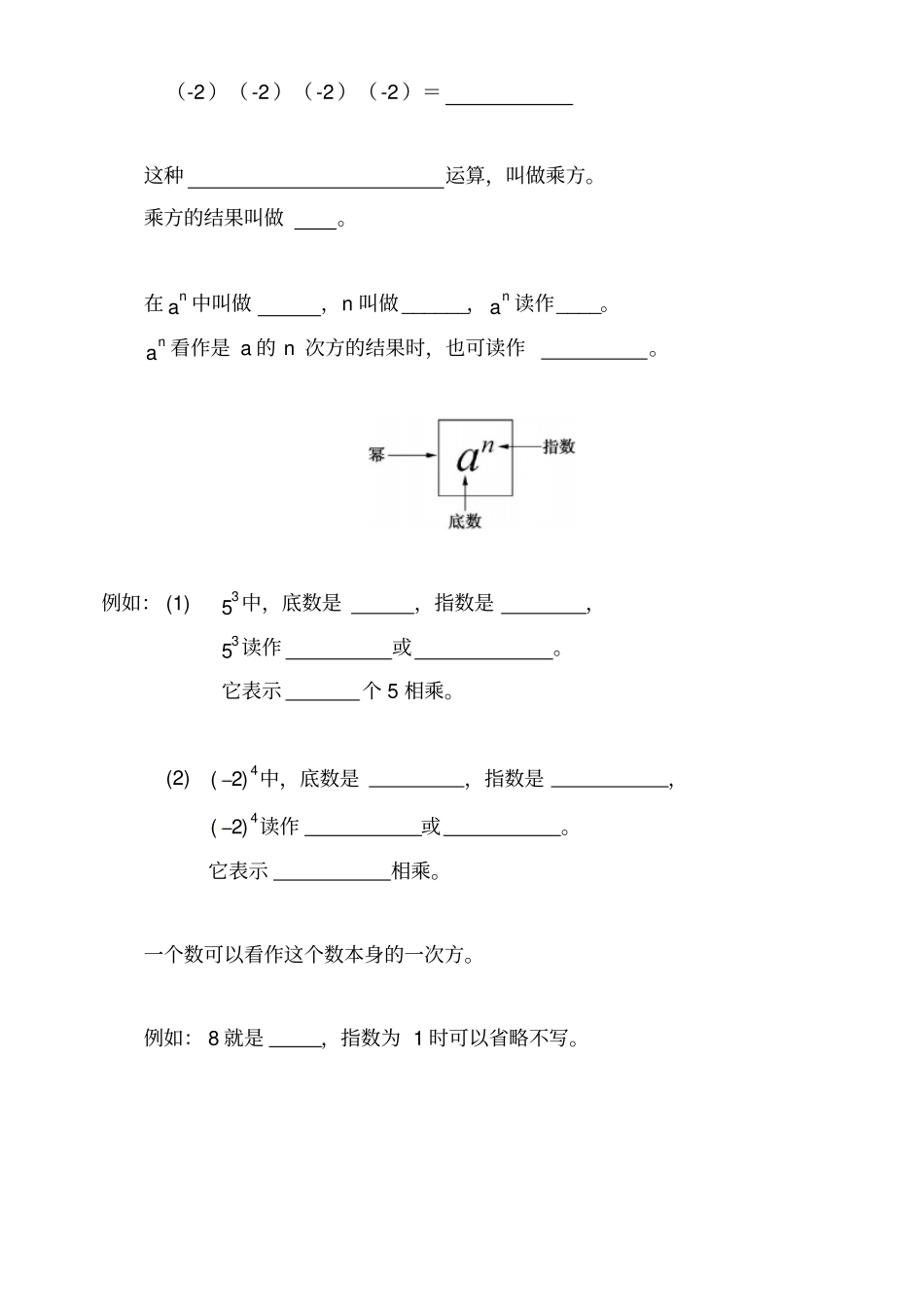
第二章有理数第十七课时§2.11 有理数的乘方班别: ________姓名: ________学号: ____日期: ____年__月__日一、学习目标1、在现实背景中,理解有理数乘方的意义。2、能进行有理数的乘方读运算。二、知识回顾:1、几个不等于零的有理数相乘,积的符号是怎样确定的?2、正方形的边长为Z,则面积积是多少?若边长为a 呢?其面积为多少?三、学习新知识: a · a= ,读作(或)a· a· a= ,读作(或)一般地,几个相同的因数a 相乘:个naaaa记作: _____________________ 例如: 2· 2· 2 =(-2 )( -2 )( -2 )( -2 )=这种运算,叫做乘方。乘方的结果叫做。在 an 中叫做,n 叫做 ______, an 读作____。an 看作是 a 的 n 次方的结果时,也可读作。例如: (1) 53中,底数是,指数是,53读作或。它表示个 5 相乘。(2) )2(4中,底数是,指数是,)2(4读作或。它表示相乘。一个数可以看作这个数本身的一次方。例如: 8 就是,指数为 1 时可以省略不写。例题:计算:(1))2(3(2))2(4(3))2(5(4) 53解:( 1))2(3 = (-2 )( -2 )( -2 )= (2)(3)(4)问:从以上计算,你能发现正数幂的特点与负数幂的特点吗?答:根据有理数乘法则,有: 正数的任何次幂都是,负数的 奇数幂 是,负数的偶次幂是。练习:)2(6读作,其中底数是,指数是。)2(6是(填正数或负数)思考:2332与有什么不同?2233与-)(-的意义是否相同?其结果是否一样?2244与-)(-呢?535322与呢?分别算出它们的结果。解:四、分层练习【A组】1 . 把下列各式写乘方的形式。(1)6×6×6=(2)2.1 ×2.1 =(3)(- 3)(- 3)(- 3)(- 3)=(4)2121212121_______________ 2. 填空:(直接写出结果)34 =231=51 =101=1001=51 =32.0=254=254 =【B组】3、3 的平方是, -3 的平方是, 平方得 9 的数有个,4、4)3(= ,272 = 2322 = ,532121= 【C组】计算:5、222432211 6、32331942