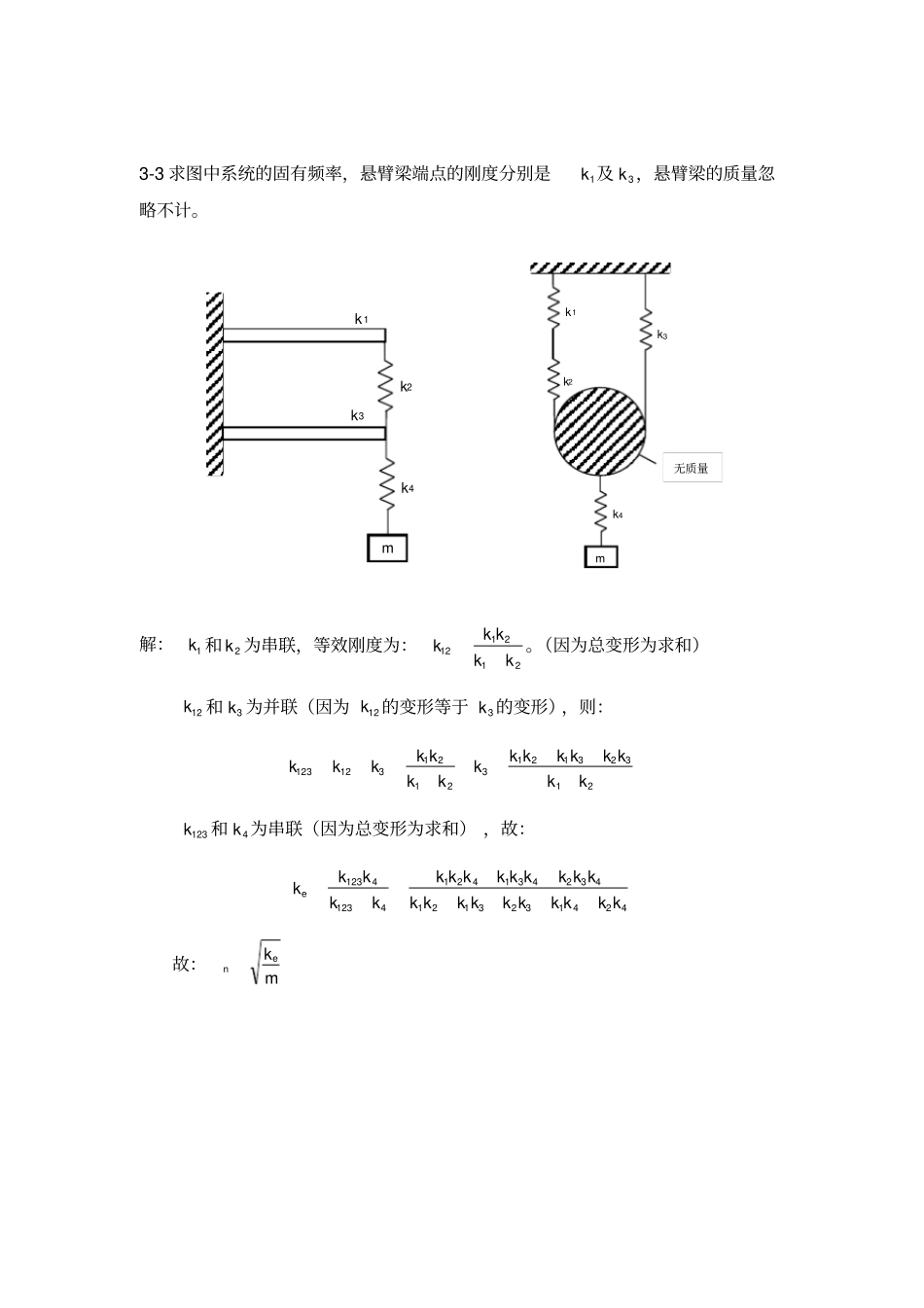
3-1 某弹簧质量系统1k ,m,具有自然频率1f,第 2 个弹簧2k 串联于第一个弹簧,其自然频率降至 1/21f ,求以1k 表示的2k 。解:1112kfm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯. (1) 121212111k kkkkkk1221121122()k kffm kk⋯⋯⋯⋯⋯⋯⋯⋯⋯ (2) 122(1)2(2)kkk,则123kk3-2 如图所示,杆 a 与弹簧1k 和2k 相连,弹簧3k 置于杆 a 的中央,杆 b 与弹簧3k和4k相连,质量 m 置于杆 b 的中央。设杆 a 和杆 b 为质量和转动惯矩可忽略的刚性杆,并能在图示平面内自由移动和转动。求质量m 上、下振动的固有频率。解:1114xk2214xk1233122xxxk4412xk12341111161644exkkkk1234111111161644eekxkkkk所以n1234114111122()44ekfmmkkkk(2)nf3-3 求图中系统的固有频率,悬臂梁端点的刚度分别是1k 及3k ,悬臂梁的质量忽略不计。解:1k 和2k 为串联,等效刚度为:212112kkkkk。(因为总变形为求和)12k和3k 为并联(因为12k 的变形等于3k 的变形),则:2132312132121312123kkkkkkkkkkkkkkkk123k和4k 为串联(因为总变形为求和) ,故:424132312143243142141234123kkkkkkkkkkkkkkkkkkkkkkkke故:mken无质量m k1k2k3k4m k 1k2k3k43-4 求图所示系统的固有频率,刚性杆的质量忽略不计。解:m 的位置:AAxkmgxxx22aFmgl1 ,amglF1,11akmglxlaxxA1,1221kamglxalx AmgkkaklkamgkalkkamglkmgxxxA212221212221222212212212klkakkake,mkenF1mg x1xAk1k2m a l 3-5 在图所示的系统中,已知bamiki,,3,2,1和,横杆质量不计。求固有频率。解:对 m 进行受力分析可得:33xkmg,即33kmgx如图可得:22221111,kbamgakFxkbamgbkFxmgkkbakbkabaxxaxxxx21222121211022120323e12a kb k11xxxmgmgkkabk k则等效弹簧刚度为:2123223123212kkbakkbkkakkkbake则固有频率为:222132212321bkakkbakkmbakkkmkenmgbaaF 2mg abx1x2x0xmgbabF1k2k1abk3m 3-6 质量1m物体挂在弹簧/k Nm下端形成静平衡,第二个质量2m 从高度 h降落到物体1m 上,该碰撞为完全弹性碰撞,如图所示,求碰撞后下方质量的运动。解:由1m 的静平衡位置得位移:x由撞击后12mm 为自由体,分析力系动平衡,得到振动的运动平衡方程:122()mmxm gkx一般解:2cossintm gxAtBtk其中12kmm2m 从高度 h 处落下,其速度有能量守恒:222212m ghm v ,得到22vgh 。1m ,2m 碰撞后,由于2m 不反弹(完全弹性碰撞) ,所以能量守恒并不适用,根据动量...