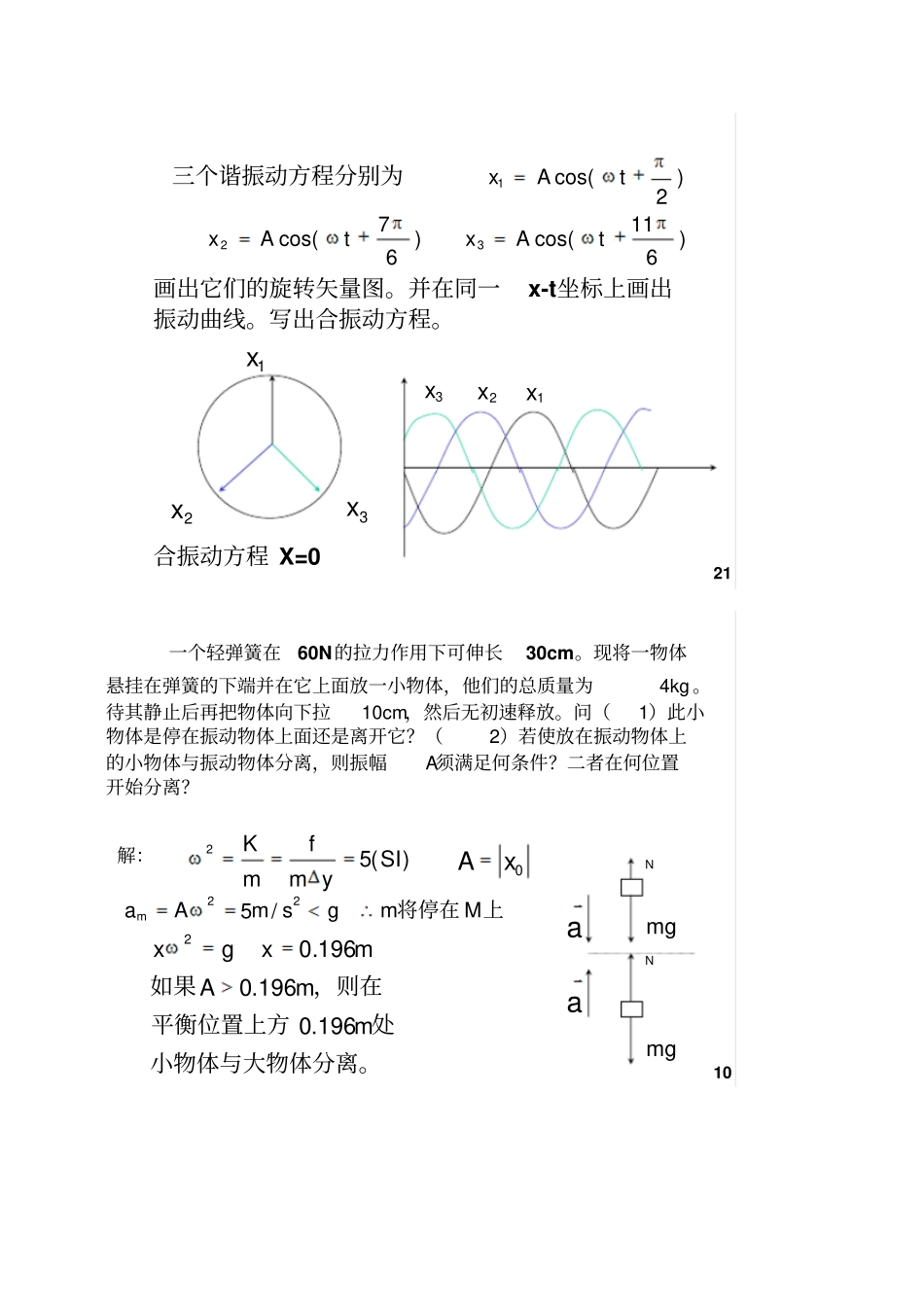
21三个谐振动方程分别为)tcos(Ax6113)tcos(Ax21)tcos(Ax672画出它们的旋转矢量图。并在同一x-t坐标上画出振动曲线。写出合振动方程。3x2x1x3x2x1x合振动方程 X=010一个轻弹簧在60N的拉力作用下可伸长30cm。现将一物体)(52SIymfmK上将停在 MmgsmAam22/5mgmgNNaa小物体与大物体分离。处平衡位置上方,则在如果mmAmxgx196.0196.0196.02悬挂在弹簧的下端并在它上面放一小物体,他们的总质量为4kg 。待其静止后再把物体向下拉10cm,然后无初速释放。问(1)此小物体是停在振动物体上面还是离开它?(2)若使放在振动物体上的小物体与振动物体分离,则振幅A须满足何条件?二者在何位置开始分离?解:0xA9在一轻弹簧下端悬挂 m0=100克砝码时,弹簧伸长8厘米,现在这根弹簧下悬挂m=250克的物体。将物体从平衡位置向下拉动 4厘米并给予向上的 21厘米 /秒的初速度。选 X轴向下,求振动的表达式。m/N...lgmk08089100解:s/rad.....mk072500808910s/m.vm.x21004000m./vxA05022020rad.xvtg640001)SI)(.tcos(.x6407050象限第象限第象限第13104100,tg,x15弹簧的串并联22112121kFkFkFxxxFFF串联:21111kkk22112121xkxkFFFxxx并联:21kkk思考1:等分n段,每段 k0=?思考2:n段串联,等效 k0=?K 0=nkK 0=k/n2.1 弹簧下悬挂一物体,弹簧静伸长为。设将物体向下拉,使弹簧有静伸长3 ,然后无初速度地释放,求此后的运动方程。解:设物体质量为 m ,弹簧刚度为 k ,则:mgk,即://nkmg取系统静平衡位置为原点0x,系统运动方程为:00020mxkxxx(参考教材 P14)解得:( )2 cosnx tt2.2 弹簧不受力时长度为65cm,下端挂上 1kg 物体后弹簧长 85cm。设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。解:由题可知:弹簧的静伸长0.850.650.2()m所以:9.87(/ )0.2ngrads取系统的平衡位置为原点,得到:系统的运动微分方程为:20nxx其中,初始条件:(0)0.2(0)0xx(参考教材 P14)所以系统的响应为:( )0.2cos()nx tt m弹簧力为:( )( )cos()knmgFkx tx tt N因此:振幅为 0.2m、周期为 2( )7s 、弹簧力最大值为1N。2.3 重物1m 悬挂在刚度为 k 的弹簧上并处于静平衡位置,另一重物2m 从高度为 h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x,则当 m有 x 位移时,系统有:2121 ()2TEmmx212Ukx由 ()0Td ...