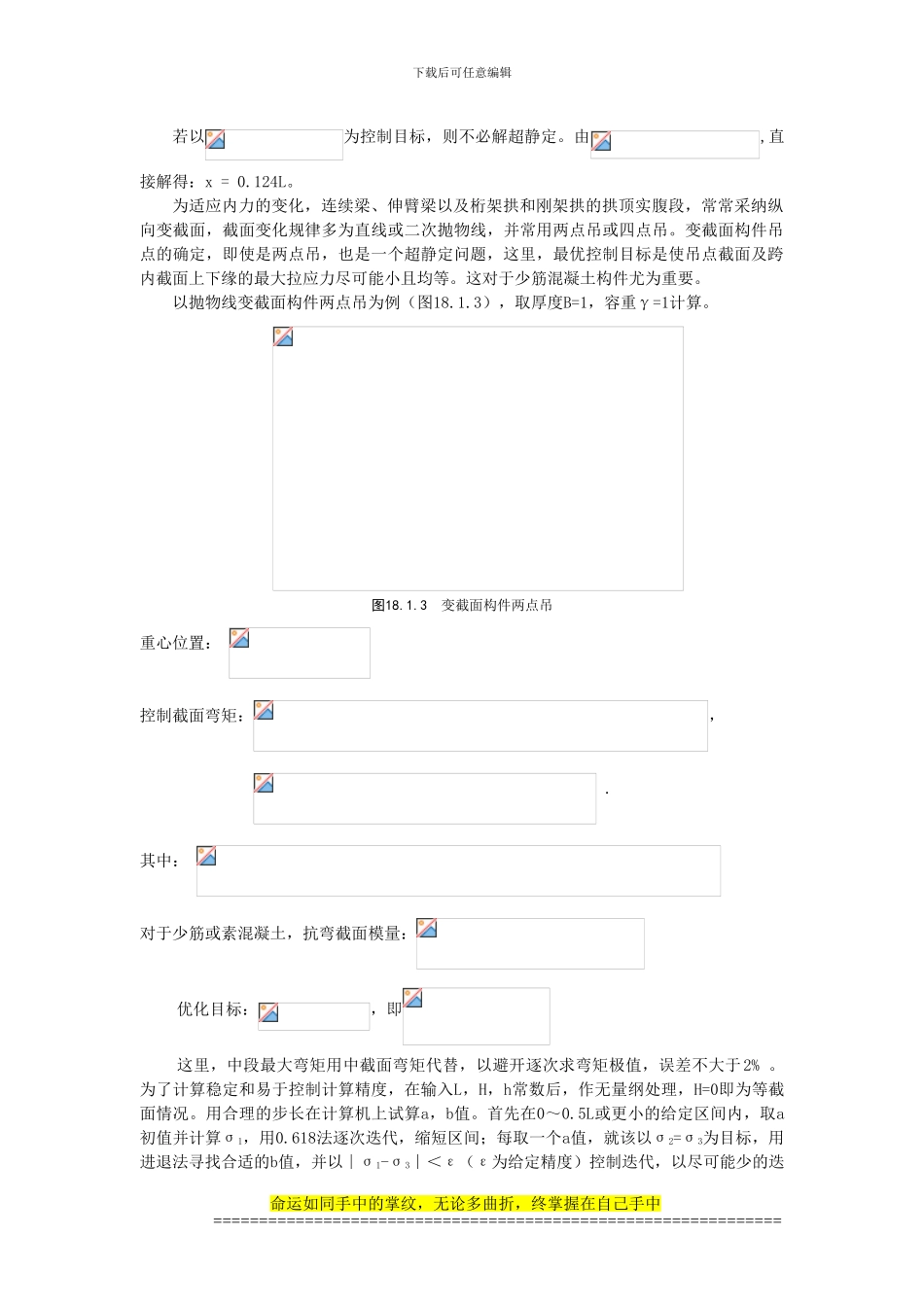
下载后可任意编辑结构施工与力学缆索吊装的最佳吊点桥梁工程施工中,当上部构件(如梁节段或拱肋等)需跨越深水、深谷、通航河道或者限于工期必须在洪汛期内架设时,常采纳无支架施工,其中更多采纳缆索分段吊装。预制构件在吊移、搁置和拼装过程中,构件的受力状态往往与成桥使用状态不同,构件的吊点(吊环)位置与数量,应在设计中确定或在施工前验算。梁段和拱肋通常采纳两点吊,当构件分段或曲率较大时,宜采纳四点吊(图18.1.1)。最佳吊点位置主要按构件吊运时的稳定与合理受力来确定,尽管有时还需要综合各种次要因素的影响。这里,以最大拉应力为控制目标,选择缆索吊装中的最佳吊点,得出等截面四吊点的位置。对于两点吊和四点吊的变截面构件超静定问题,用寻优迭代的方法和总和试算法[19],可得出吊点的变化规律和有用的计算结果。图18.1.1 刚架拱桥吊装分段构件均近似按直梁验算。当构件截面上下配置相等钢筋并采纳两吊点时,构件受力特点如双伸臂简支梁,吊点宜对称布置,控制目标为两吊点处最大负弯矩M1与跨中最大正弯矩M2绝对值相等(亦即最大拉应力相等),由此可解得 x=0.207L(L为拱肋构件长度)。考虑斜索产生偏心拉压、上下缘配筋数量、端头接口及弯拱肋重心位置等因素后,实际吊点位置选在距拱肋端0.22L左右(L为拱肋构件长度)。当桥梁跨径大,吊装设备吨位许可时,可按较长的分段预制拱肋(特别是拱顶段),以减少空中操作;当拱段曲率较大时,也采纳四点吊,并使用转向滑轮。四吊点构件受力是超静定问题.利用对称性取半结构后,按一次超静定梁分析.选如图18.1.2所示的基本体系,多余未知力X1即为构件中部的正弯矩M1,力法方程为δ11X1+Δ1P =0 。设外侧吊点距杆端为x,考虑施工方便,一般取内外侧吊点间距为0.2L(小于0.27L时,其跨间弯矩均较小).用图乘法计算主系数δ11和自由项Δ1P后,可求得 。图18.1.2 基本体系简化命运如同手中的掌纹,无论多曲折,终掌握在自己手中==============================================================下载后可任意编辑若以为控制目标,则不必解超静定。由,直接解得:x = 0.124L。为适应内力的变化,连续梁、伸臂梁以及桁架拱和刚架拱的拱顶实腹段,常常采纳纵向变截面,截面变化规律多为直线或二次抛物线,并常用两点吊或四点吊。变截面构件吊点的确定,即使是两点吊,也是一个超静定问题,这里,最优控制目标是使吊点截面及跨内截面上下缘的最大拉应力尽可能小且均等。这...