2016年立体几何高考题汇总VIP免费

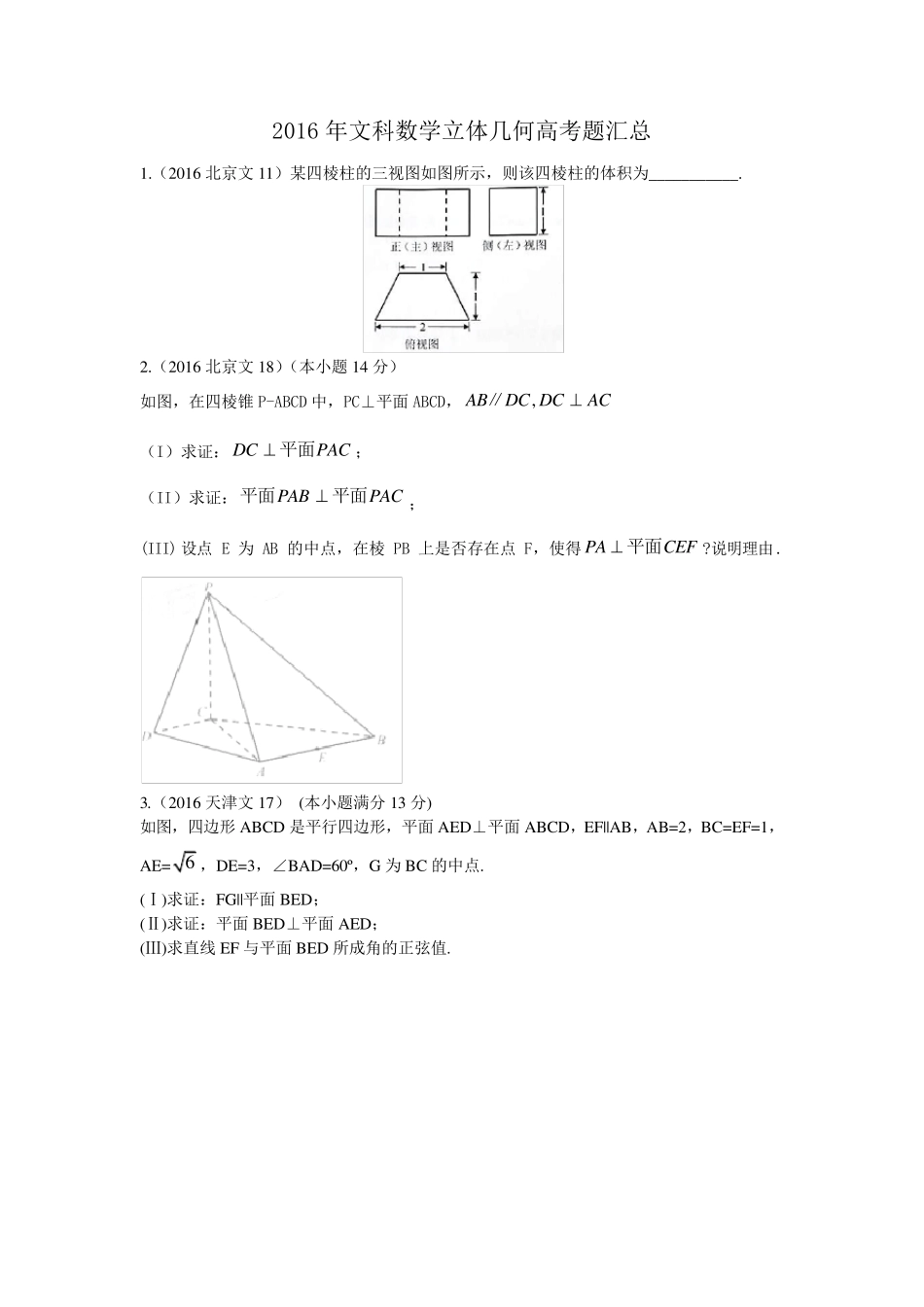
2016 年文科数学立体几何高考题汇总 1.（2016 北京文11）某四棱柱的三视图如图所示，则该四棱柱的体积为___________. 2.（2016 北京文18）（本小题14 分） 如图，在四棱锥P-ABCD 中，PC⊥平面ABCD，,ABDC DCAC∥ （I）求证：DCPAC 平面； （II）求证：PABPAC平面 平面； (III) 设点E 为AB 的中点，在棱PB 上是否存在点F，使得PACEF 平面?说明理由. 3.（2016 天津文17） (本小题满分13 分) 如图，四边形ABCD 是平行四边形，平面AED⊥平面ABCD，EF||AB，AB=2，BC=EF=1，AE= 6 ，DE=3，∠BAD=60º，G 为BC 的中点. (Ⅰ)求证：FG||平面BED； (Ⅱ)求证：平面BED⊥平面AED； (Ⅲ)求直线 EF 与平面BED 所成角的正弦值. 【答案】（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ） 65 【解析】 试题分析：（Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行寻找与论证，往往结合平几知识，如本题构造一个平行四边形：取 BD 的中点为O ，可证四边形OGFE 是平行四边形，从而得出OEFG //（Ⅱ）面面垂直的证明，一般转化为证线面垂直，而线面垂直的证明，往往需多次利用线面垂直判定与性质定理，而线线垂直的证明有时需要利用平几条件，如本题可由余弦定理解出09 0ADB，即ADBD （Ⅲ）求线面角，关键作出射影，即面的垂线，可利用面面垂直的性质定理得到线面垂直，即面的垂线：过点 A 作DEAH 于点 H ，则AH平面 BED ，从而直线 AB 与平面 BED所成角即为ABH.再结合三角形可求得正弦值 试题解析：（Ⅰ）证明：取 BD 的中点为O ，连接OGOE,，在 BCD中，因为G 是 BC 的中点，所以DCOG //且121DCOG，又因为DCABABEF//,//，所以OGEF //且OGEF  ，即四边形OGFE 是平行四边形，所以OEFG //，又FG平面 BED ，OE平面 BED ，所以//FG平面 BED . （Ⅱ）证明：在 ABD中，06 0,2,1BADABAD，由余弦定理可3BD，进而可得09 0ADB，即ADBD ，又因为平面AED平面BDABCD,平面 ABCD；平面AED平面ADABCD ，所以BD平面 AED.又因为BD平面 BED ，所以平面BED平面 AED. （Ⅲ）解：因为ABEF //，所以直线 EF 与平面 BED 所成角即为直线 AB 与平面BED 所成角.过点 A 作DEAH 于点 H ，连接 BH ，又因为平面BED平面EDAED ，由（Ⅱ）知AH平面 BED ，所以直线 AB 与平面 BED 所成角...