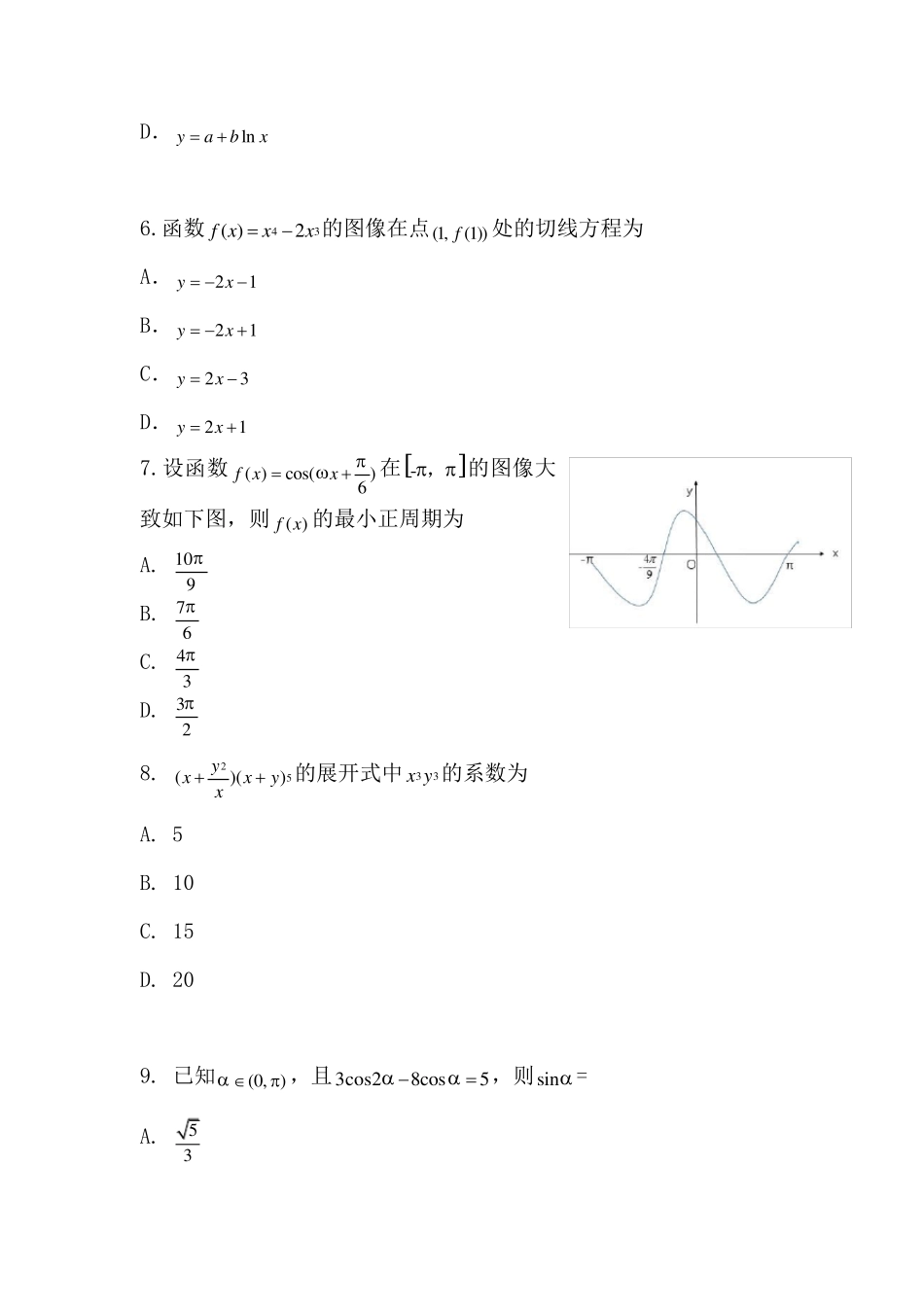
2020年普通高等学校招生全国统一考试 理科数学 一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1. 若1zi ,则22zz A.0 B.1 C.2 D.2 2.设集合240Ax x,20Bxxa,且21ABxx ,则a A.-4 B.-2 C.2 D.4 3. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为 A. 514 B. 512 C. 514 D. 512 4.已知A为抛物线2:2(0)C ypx p上一点,点A到C的焦点的距离为12,到y 轴的距离为9,则p A.2 B.3 C.6 D.9 5.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x(单位:C)的关系,在20 个不同的温度条件下进行种子发芽实验,由实验数据ii( ,)x y(1,2,...,20)i 得到下面的散点图: 由此散点图,在10℃至 40℃之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是 A.yabx B.2yabx C.xyabe D. lnyabx 6.函数 43( )2f xxx的图像在点(1,(1))f处的切线方程为 A.21yx B.21yx C.23yx D.21yx 7.设函数( )cos()6f xx在-,的图像大致如下图,则( )f x 的最小正周期为 A. 109 B. 76 C. 43 D. 32 8. 25()()yxxyx的展开式中33x y 的系数为 A. 5 B. 10 C. 15 D. 20 9. 已知(0, ) ,且3cos28cos5 ,则sin = A. 53 B. 23 C. 13 D. 59 10. 已知,,A B C 为球O的球面上的三个点,1O 为ABC的外接圆,若1O 的面积为14 , ABBCACOO,则球O的表面积为 A. 64 B. 48 C. 36 D. 32 11. 已知22:2220M xyxy ,直线 l: 2x+y+2=0,p 为l 上的动点.过点 p 作M 的切线 PA ,PB ,切点为,A B ,当 PM AB 最小时,直线 AB的方程为 A. 210xy B. 210xy C. 210xy D. 210xy 12.若a242log42logbab则 A.a>2b B.a<2b C.a>2b D.a<2b 二、填空题:本题共 4 小题,每小题 5 分,共 20 分。 13.若x,y 满足约束条件220,10,10,xyxyy ...