MATLAB中简单的数据拟合方法与应用实例①VIP免费

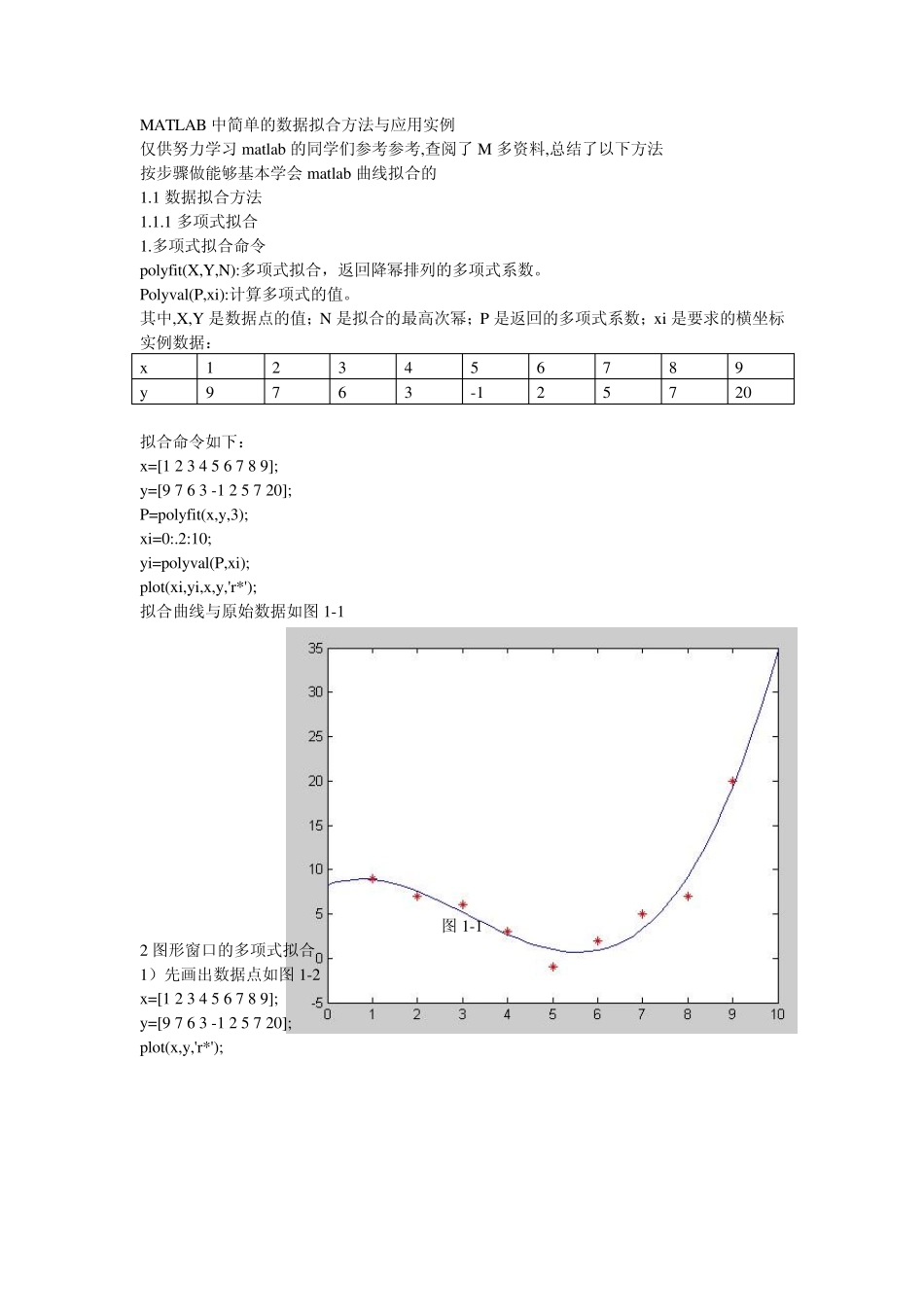
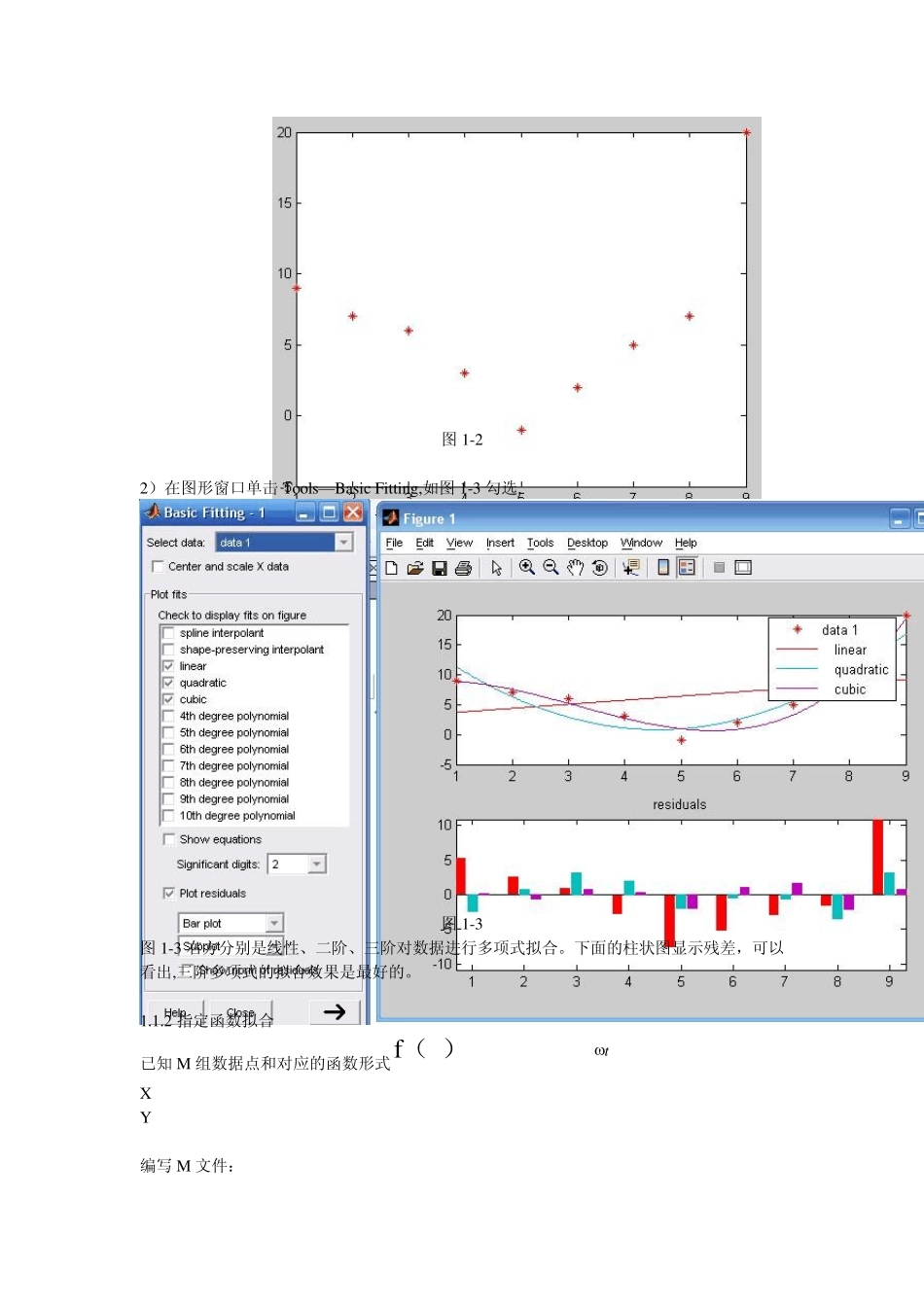
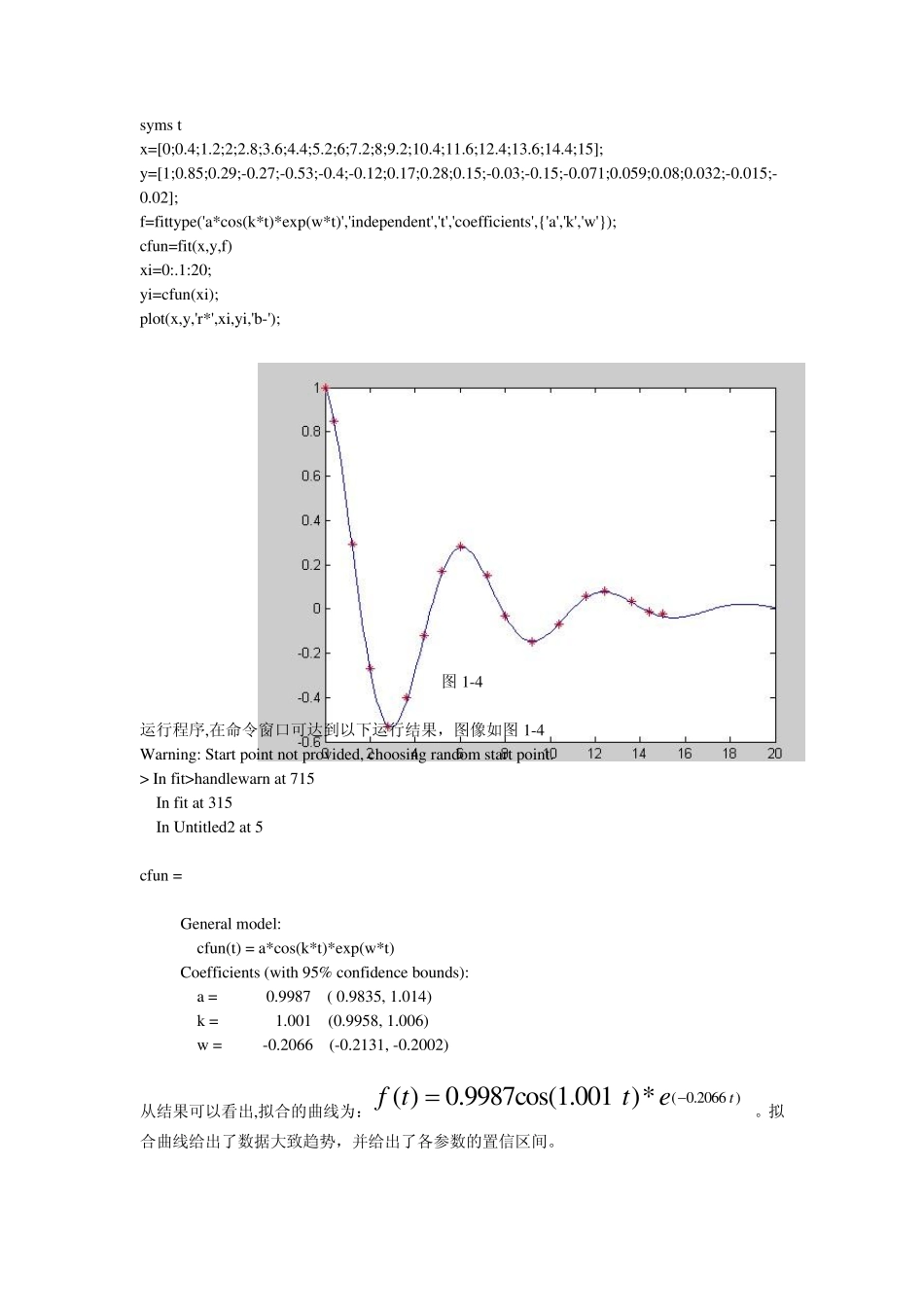
MATLAB 中简单的数据拟合方法与应用实例 仅供努力学习matlab 的同学们参考参考,查阅了M 多资料,总结了以下方法 按步骤做能够基本学会matlab 曲线拟合的 1.1 数据拟合方法 1.1.1 多项式拟合 1.多项式拟合命令 poly fit(X,Y,N):多项式拟合，返回降幂排列的多项式系数。 Poly v al(P,x i):计算多项式的值。 其中,X,Y 是数据点的值；N 是拟合的最高次幂；P 是返回的多项式系数；x i 是要求的横坐标 实例数据： x 1 2 3 4 5 6 7 8 9 y 9 7 6 3 -1 2 5 7 20 拟合命令如下： x =[1 2 3 4 5 6 7 8 9]; y =[9 7 6 3 -1 2 5 7 20]; P=poly fit(x ,y ,3); x i=0:.2:10; y i=poly v al(P,x i); plot(x i,y i,x ,y ,'r*'); 拟合曲线与原始数据如图 1-1 图 1-1 2 图形窗口的多项式拟合 1）先画出数据点如图 1-2 x =[1 2 3 4 5 6 7 8 9]; y =[9 7 6 3 -1 2 5 7 20]; plot(x ,y ,'r*'); 图1-2 2）在图形窗口单击Tools—Basic Fitting,如图1-3 勾选. 图1-3 图1-3 右方分别是线性、二阶、三阶对数据进行多项式拟合。下面的柱状图显示残差，可以看出,三阶多项式的拟合效果是最好的。 1.1.2 指定函数拟合 已知 M 组数据点和对应的函数形式ft（t）=acos(kt)e X Y 编写 M 文件： syms t x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15]; y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02]; f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'}); cfun=fit(x,y,f) xi=0:.1:20; yi=cfun(xi); plot(x,y,'r*',xi,yi,'b-'); 图1-4 运行程序,在命令窗口可达到以下运行结果，图像如图1-4 Warning: Start point not provided, choosing random start point. > In fit>handlewarn at 715 In fit at 315 In Untitled2 at 5 cfun = General model: cfun(t) = a*cos(k*t)*exp(w*t) Coefficients (with 95% confidence bounds): a = 0.9987 ( 0.9835, 1.014) k = 1.001 (0.9958, 1.006) w = -0.2066 (-0.2131, -0.2002) 从结果可以看出,拟合的曲线为：( 0.2066 )( )0.9987cos(1.001 )*tf tte  。拟合曲线给出了数据大致趋势，并给出了各参数的置信...