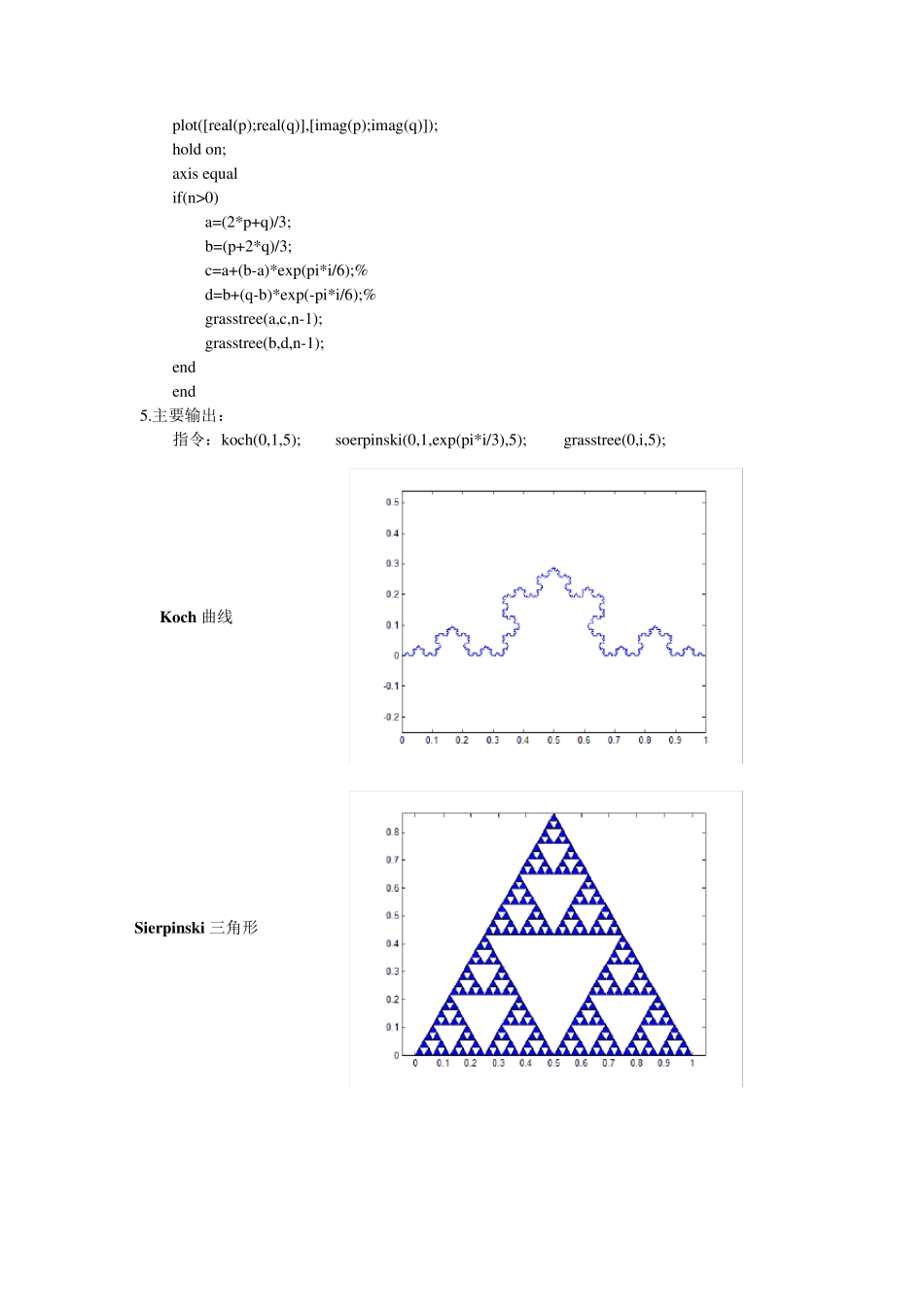
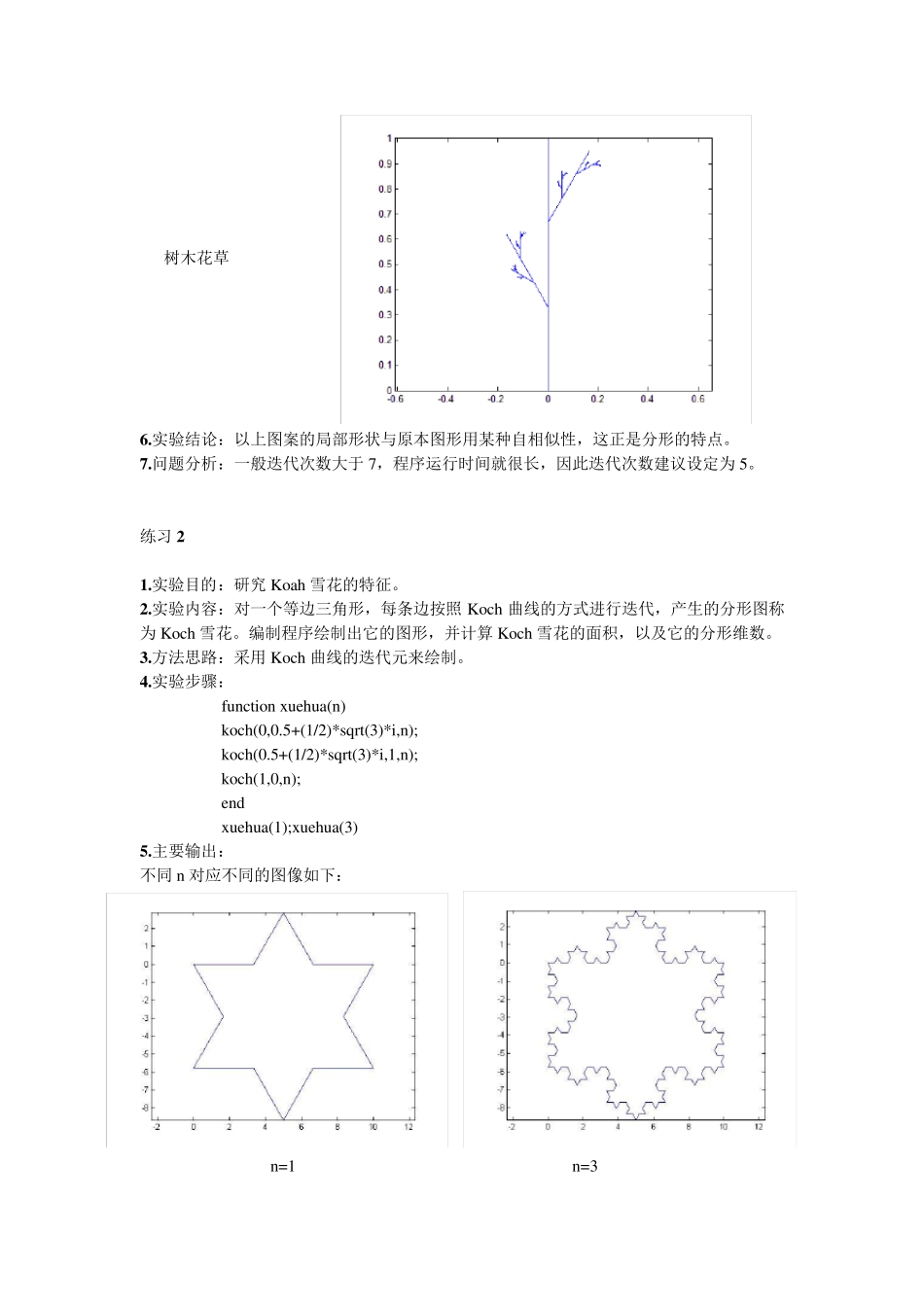
数学实验报告:分形迭代 练习1 1.实验目的:绘制分形图案并分析其特点。 2.实验内容:绘制Koch 曲线、Sierpinski 三角形和树木花草图形,观察这些图形的局部和原来分形图形的关系。 3.实验思路:利用函数反复调用自己来模拟分形构造时的迭代过程,当迭代指标 n 为 0 时运行作图操作,否则继续迭代。 4.实验步骤: (1)Koch 曲线 fu nction koch(p,q,n) % p、q 分别为 koch 曲线的始末复坐标,n 为迭代次数 if (n==0) plot([real(p);real(q)],[imag(p);imag(q)]); hold on; ax is equ al else a=(2*p+q)/3; % 求出从 p 到 q 的 1/3 处端点 a b=(p+2*q)/3; % 求出从 p 到 q 的 2/3 处端点 b c=a+(b-a)*ex p(pi*i/3);% koch(p, a, n-1); % 对 pa 线段做下一回合 koch(a, c, n-1); % 对 ac 线段做下一回合 koch(c, b, n-1); % 对 cb 线段做下一回合 koch(b, q, n-1); % 对 bq 线段做下一回合 end (2)Sierpinski 三角形 fu nction sierpinski(a,b,c,n) % a、b、c 为三角形顶点,n 为迭代次数 if (n==0) fill([real(a) real(b) real(c)],[imag(a) imag(b) imag(c)],'b');% 填充三角形abc hold on; ax is equ al else a1=(b+c)/2; b1=(a+c)/2; c1=(a+b)/2; sierpinski(a,b1,c1,n-1); sierpinski(a1,b,c1,n-1); sierpinski(a1,b1,c,n-1); end (3)树木花草 fu nction grasstree(p,q,n) % p、q 分别为树木花草始末复坐标,n 为迭代次数 plot([real(p);real(q)],[imag(p);imag(q)]); hold on; ax is equ al if(n>0) a=(2*p+q)/3; b=(p+2*q)/3; c=a+(b-a)*ex p(pi*i/6);% d=b+(q-b)*ex p(-pi*i/6);% grasstree(a,c,n-1); grasstree(b,d,n-1); end end 5.主要输出: 指令:koch(0,1,5); soerpinski(0,1,ex p(pi*i/3),5); grasstree(0,i,5); Koch 曲线 Sierpinski 三角形 树木花草 6 .实验结论:以上图案的局部形状与原本图形用某种自相似性,这正是分形的特点。 7 .问题分析:一般迭代次数大于 7,程序运行时间就很长,因此迭代次数建议设定为 5。 练习 2 1 .实验目的:研究 Koah 雪花的特征。 2 .实验内容:对一个等边三角形,每条边按照 Koch 曲线的方式进行迭代,产生的分形图称为 Koch 雪花。编制程序绘制出它的图形,并计算 Koch 雪花的面积,以及它的分形维数。 3 ....