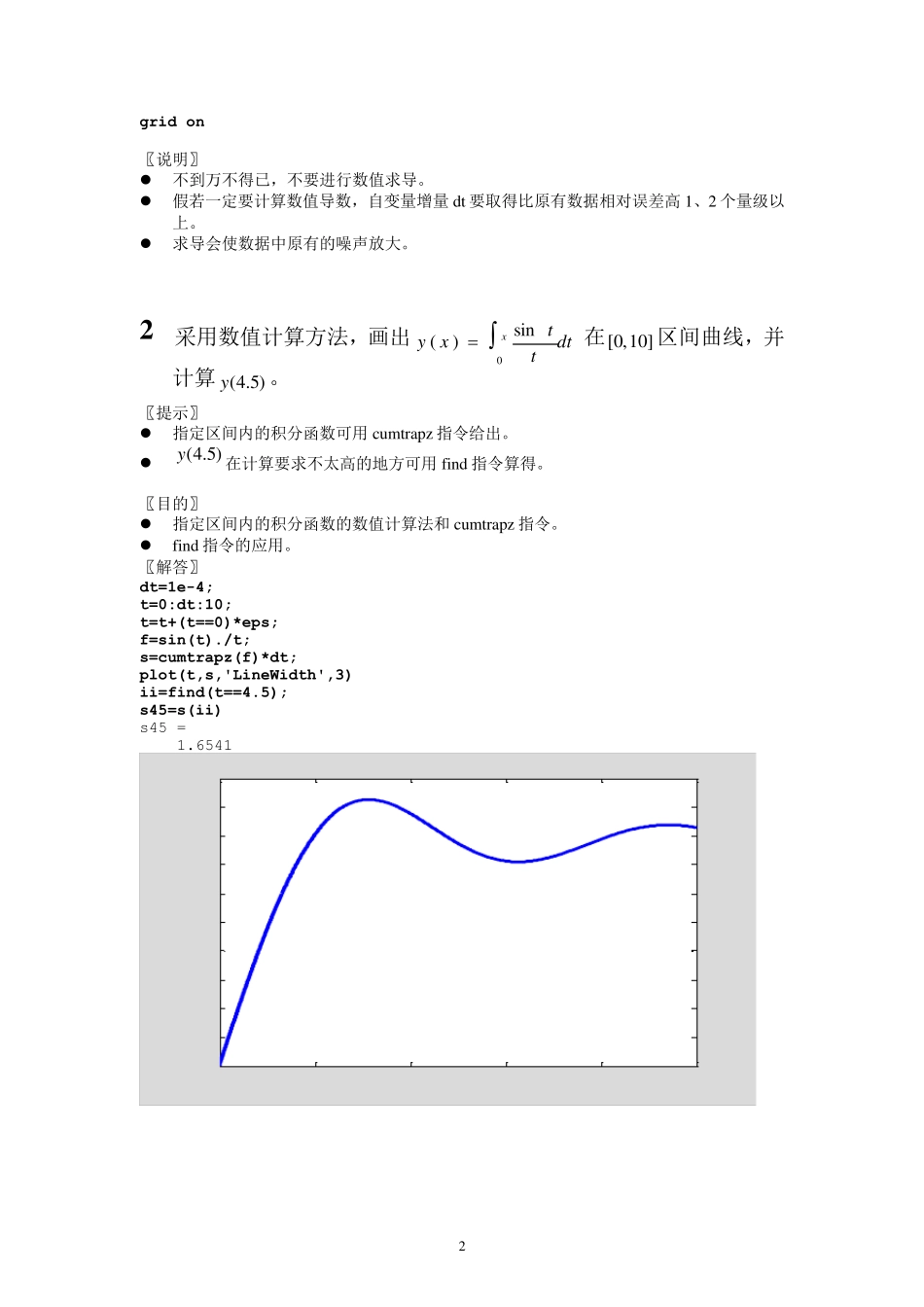
1 第4章 数值运算 习题 4 及解答 1 根据题给的模拟实际测量数据的一组t 和 )(ty试用数值差分diff或数值梯度gradient指令计算)(ty ,然后把)(ty和)(ty 曲线绘制在同一张图上,观察数值求导的后果。 ( 模拟数据从prob_data401.mat获得) 〖目的〗 强调:要非常慎用数值导数计算。 练习 mat数据文件中数据的获取。 实验数据求导的后果 把两条曲线绘制在同一图上的一种方法。 〖解答〗 (1)从数据文件获得数据的指令 假如 prob_data401.mat文件在当前目录或搜索路径上 clear load prob_data401.mat (2)用diff 求导的指令 dt=t(2)-t(1); yc=diff(y)/dt; %注意 yc 的长度将比 y 短 1 plot(t,y,'b',t(2:end),yc,'r') grid on 01234567-2-1.5-1-0.500.511.5 (3)用gradent求导的指令(图形与上相似) dt=t(2)-t(1); yc=gradient(y)/dt; plot(t,y,'b',t,yc,'r') 2 grid on 〖说明〗 不到万不得已,不要进行数值求导。 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2 个量级以上。 求导会使数据中原有的噪声放大。 2 采用数值计算方法,画出dtttxyx0sin)(在]10 ,0[区间曲线,并计算)5.4(y。 〖提示〗 指定区间内的积分函数可用 cumtrapz指令给出。 )5.4(y在计算要求不太高的地方可用 find 指令算得。 〖目的〗 指定区间内的积分函数的数值计算法和 cumtrapz指令。 find 指令的应用。 〖解答〗 dt=1e-4; t=0:dt:10; t=t+(t==0)*eps; f=sin(t)./t; s=cumtrapz(f)*dt; plot(t,s,'LineWidth',3) ii=find(t==4.5); s45=s(ii) s45 = 1.6541 024681000.20.40.60.811.21.41.61.82 3 3 求函数xexf3sin)(的数值积分 0 )(dxxfs,并请采用符号计算尝试复算。 〖提示〗 数值积分均可尝试。 符号积分的局限性。 〖目的〗 符号积分的局限性。 〖解答〗 dx=pi/2000; x=0:dx:pi; s=trapz(exp(sin(x).^3))*dx s = 5.1370 符号复算的尝试 syms x f=exp(sin(x)^3); ss=int(f,x,0,pi) Warning: Explicit integral could not be found. > In sym.int at 58 ss = int(exp(sin(x)^3),x = 0 .. pi) 4 用quad 求取dxxex sin7.15的数值积分,并保证积分的绝对精度为910 。 〖目的〗 quadl,精度可控,计算较快。 近似积...