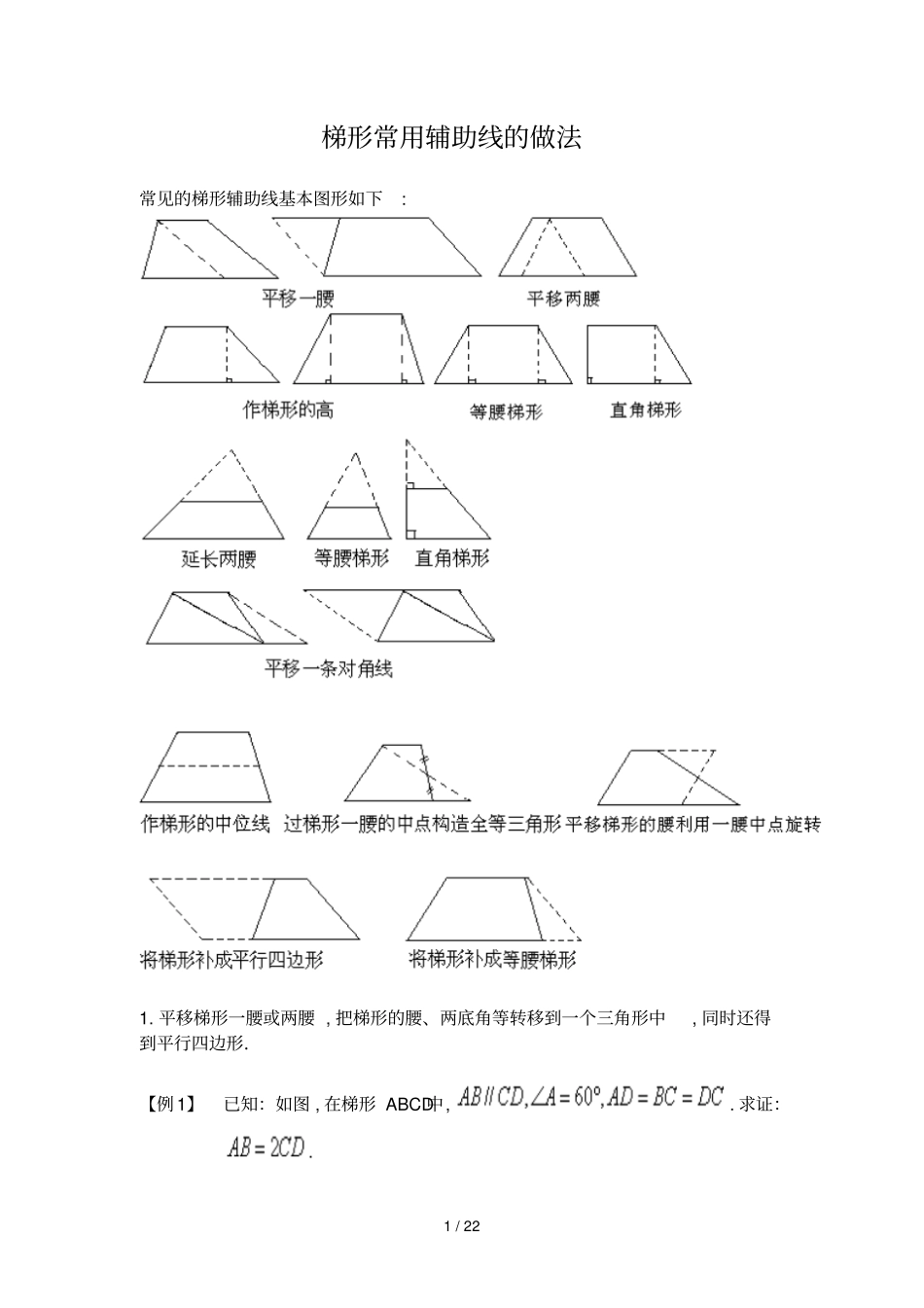
1 / 22 梯形常用辅助线的做法常见的梯形辅助线基本图形如下: 1. 平移梯形一腰或两腰 , 把梯形的腰、两底角等转移到一个三角形中, 同时还得到平行四边形.【例 1】已知:如图 , 在梯形 ABCD中,. 求证:. 2 / 22 分析 : 平移一腰 BC到 DE,将题中已知条件转化在同一等腰三角形中解决, 即AB=2CD. 证明:过 D作 , 交 AB于 E. AB 平行于 CD,且 , ∴四边形是菱形 . ∴又∴为等边三角形 . ∴又 , ∴∴. 【例 2】如图 , 在梯形 ABCD 中,AD∥BC , E 、F 分别是 AD 、BC 的中点 , 若 .AD = 7 ,BC = 15 ,求 EF .分析:由条件 , 我们通过平移 AB 、DC ;构造直角三角形MEN ,使 EF 恰好是△ MEN 的中线.解:过 E 作 EM∥AB ,EN ∥DC ,分别交 BC 于 M 、N , , 3 / 22 ∴∴是直角三角形 , , , ∴ . 、分别是、的中点 , ∴为的中点 , ∴ . 变式:如图 1,梯形 ABCD的上底 AB=3,下底 CD=8,腰 AD=4,求另一腰 BC的取值范围。图 1 析解: 过点 B 作 BM//AD 交 CD于点 M,则梯形 ABCD转化为△ BCM和平行四边形ABMD。在△BCM中, BM=AD=4,CM=CD-DM=CD-AB=8-3=5,所以 BC的取值范围是:5-4