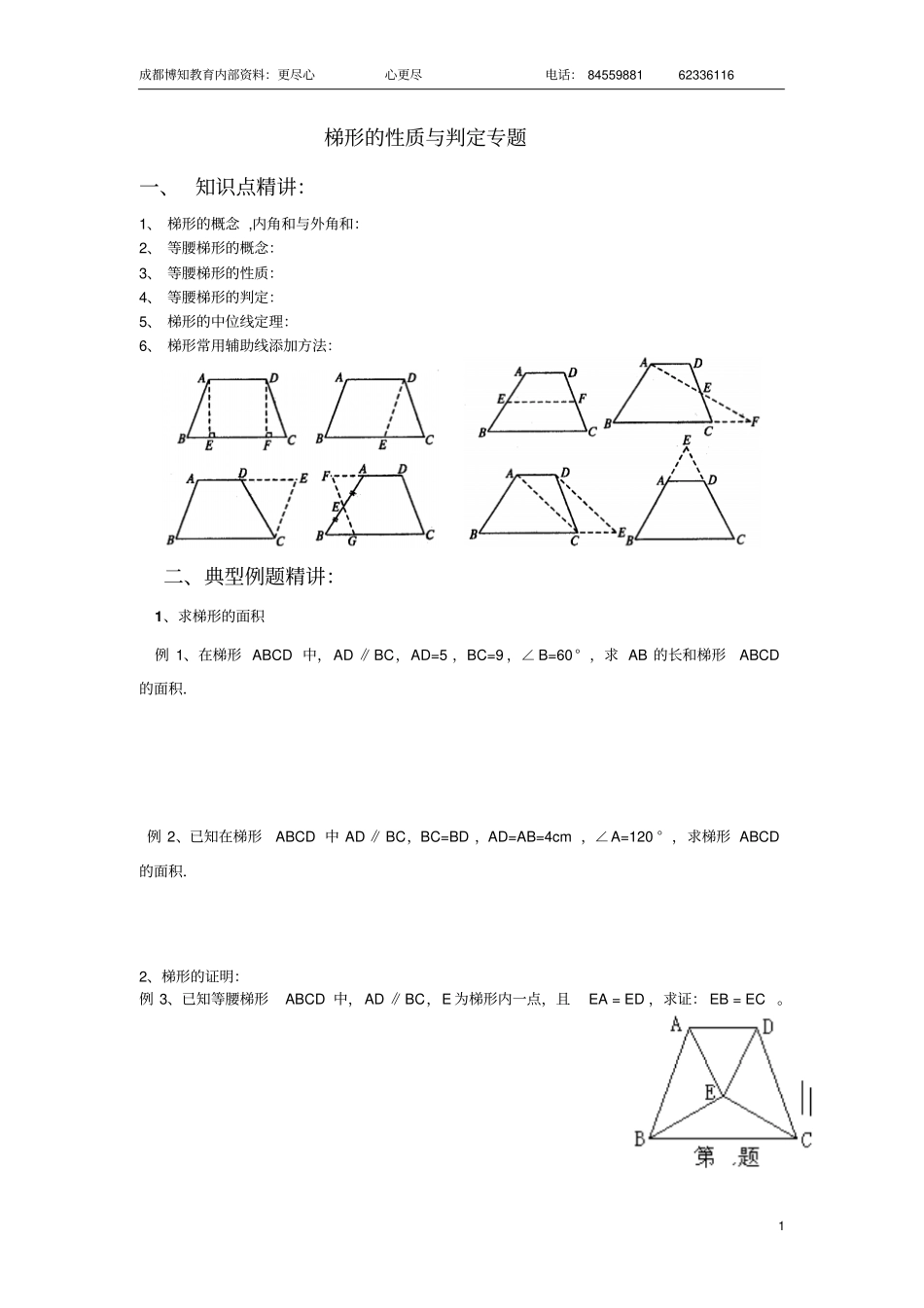
成都博知教育内部资料:更尽心心更尽电话: 84559881 62336116 1 梯形的性质与判定专题一、 知识点精讲:1、 梯形的概念 ,内角和与外角和:2、 等腰梯形的概念:3、 等腰梯形的性质:4、 等腰梯形的判定:5、 梯形的中位线定理:6、 梯形常用辅助线添加方法:二、典型例题精讲:1、求梯形的面积例 1、在梯形 ABCD 中,AD ∥BC,AD=5 ,BC=9 ,∠ B=60 ° ,求 AB 的长和梯形ABCD的面积.例 2、已知在梯形ABCD 中 AD ∥ BC,BC=BD ,AD=AB=4cm ,∠A=120 ° ,求梯形 ABCD的面积.2、梯形的证明:例 3、已知等腰梯形ABCD 中,AD ∥BC,E 为梯形内一点,且EA = ED ,求证: EB = EC 。成都博知教育内部资料:更尽心心更尽电话: 84559881 62336116 2 例 4、在等腰梯形ABCD 中,AD ∥BC,AB=DC ,点 E 是 BC 边的中点, EM⊥AB,EN⊥CD ,垂足分别为M 、N.求证: EM =EN.例 5、四边形 ABCD 是矩形, 四边形 ABDE 是等腰梯形, AE∥BD .求证:△BED ≌△ BCD .例 6、梯形 ABCD 中,∠ B+∠C=90° ,E、F 分别为上、下底的中点. 求证:)ADBC(21EF.例 7、在直角梯形ABCD 中,CDAB //,CDAD于 D,,BCAE于 E,BCAB求证:CECD。例 8、已知:如图,四边形ABCD 中, AD+B C> AB,∠ ADC 与∠ BCD 的平分线相交于AB上的一点 P,且 CP⊥DP。求证:四边形ABCD是梯形。ENMDCBAPDCBA成都博知教育内部资料:更尽心心更尽电话: 84559881 62336116 3 例 9、如图,在直角梯形ABCD 中,AB∥DC,∠ABC=900,AB=2DC,对角线 AC⊥ BD,垂足为 F,过点 F 作 EF∥ AB,交 AD于点 E,CF=4㎝。(1)、求证:四边形ABFE是等腰梯形;(2)、求 AB的长。3、拓展与探索:例 10、如图,已知在梯形ABCD 中, AD∥ BC,AB=DC,对角线 AC和 BD相交于点 O,E是 BC边上的一个动点(点E 不于 B、C两点重合),EF∥BD交 AC于点 F。EG∥AC交 BD于点 G。(1)、求证:四边形EFOG 的周长等于2OB;(2)、请将上述题目的条件“梯形ABCD中, AD∥BC,AB=DC”改为另一种四边形,其他条件不变,使得结论“四边形EFOG 的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证,不必证明。例 11、如图,在梯形ABCD 中, AD∥ BC,∠ B=900,AD=24cm,AB=8cm,BC=26cm,动点 P从 A 点开始沿 AD边以 1cm/秒的速度向D运动,动点Q从 C...