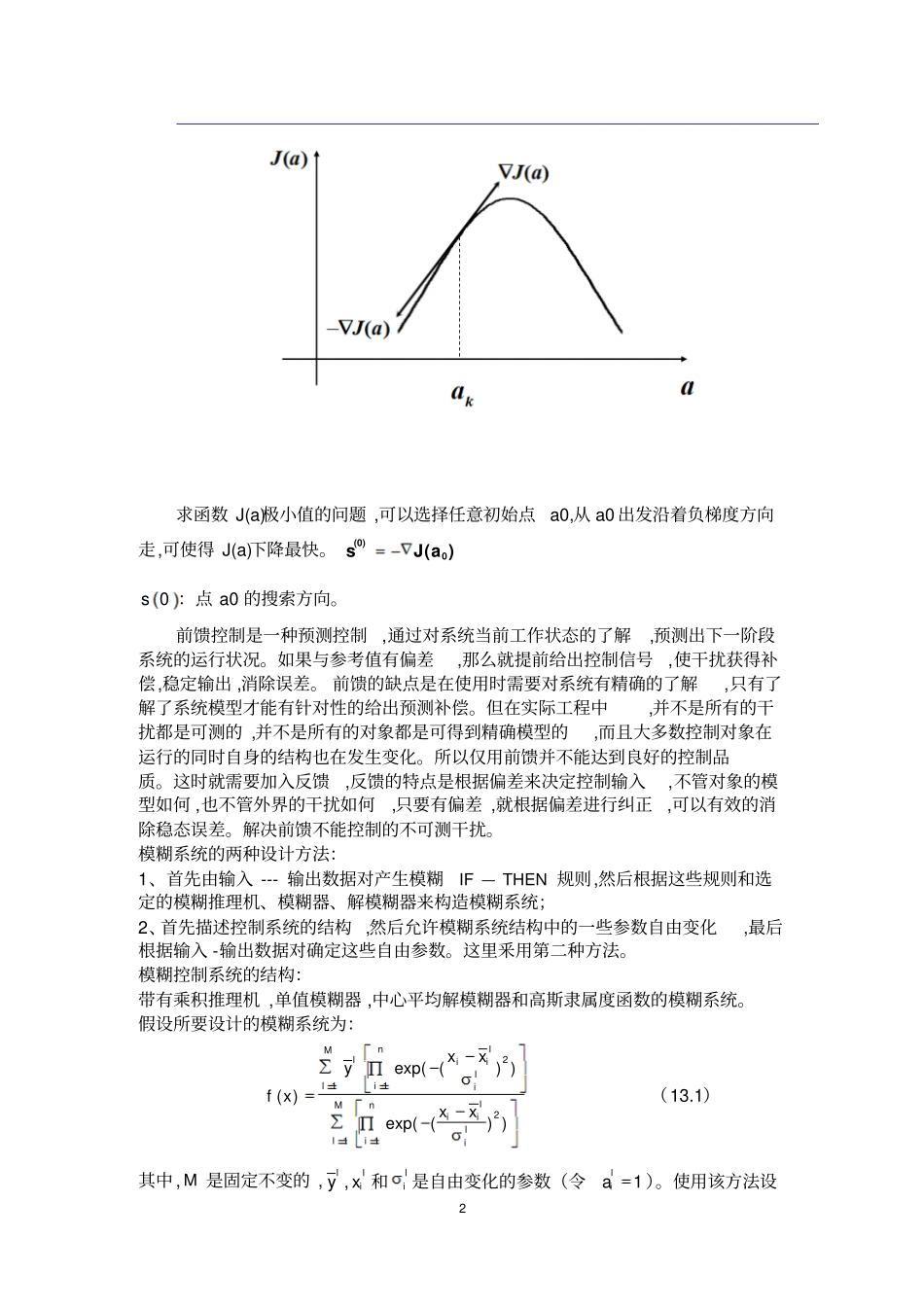
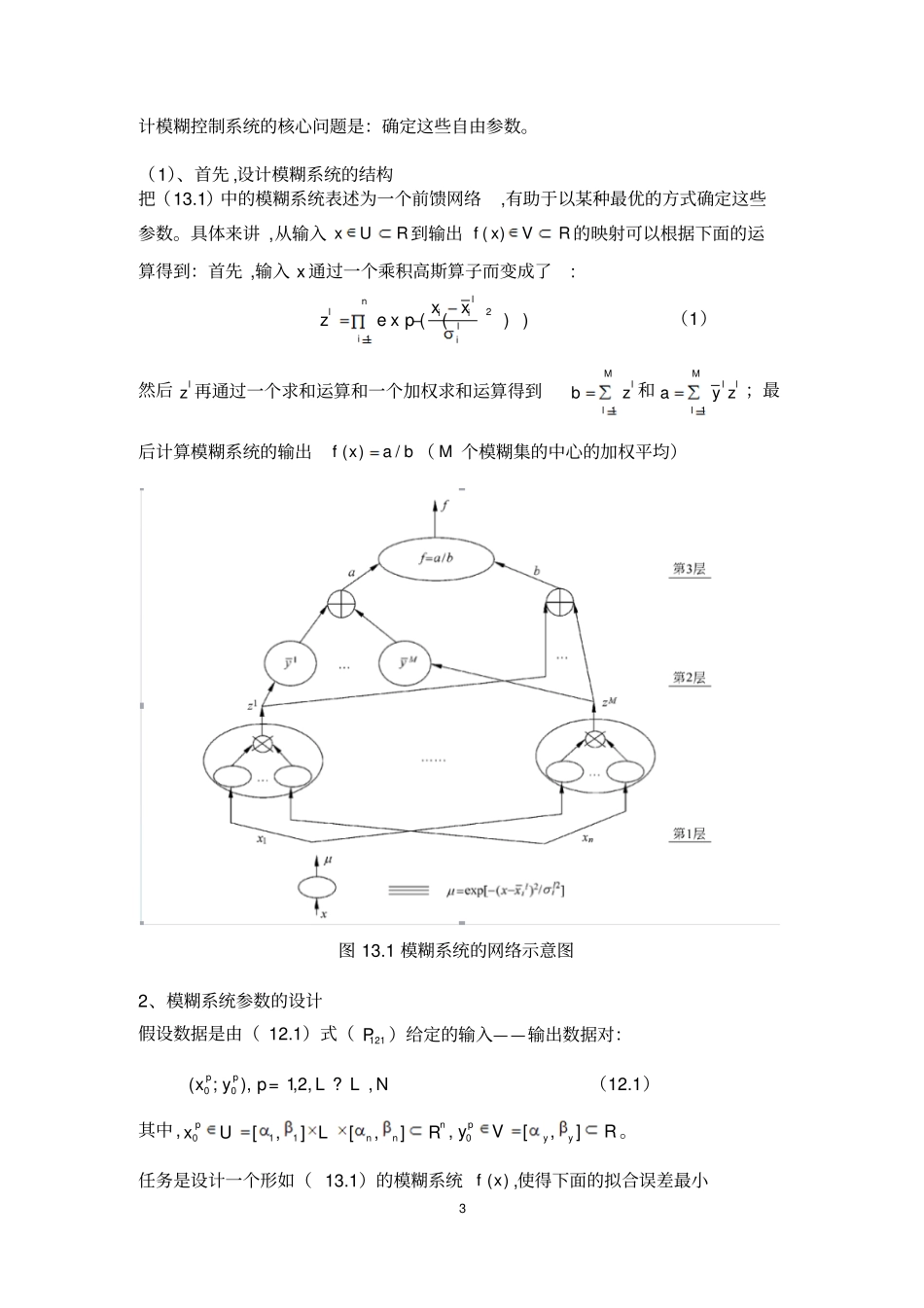
1 如何用梯度下降法设计模糊控制系统主要讲模糊系统结构的选择、 模糊系统参数的设计和在非线性动态系统辨识中的应用。在向量微积分中 ,标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。更严格的说,从欧几里得空间nR 到 R 的函数的梯度是在nR 某一点最佳的线性近似。在这个意义上,梯度是雅可比矩阵的一个特殊情况。在单变量的实值函数的情况,梯度只是导数 ,或者 ,对于一个线性函数 ,也就是线的斜率。用于斜度 ,也就是一个曲面沿着给定方向的倾斜程度,梯度的数值有时也被称为梯度。梯度下降法又称最速下降法。函数)(J a 在某点ka 的梯度是一个向量 ,其方向是 J(a)增长最快的方向。 显然 ,负梯度方向是)(J a 减少最快的方向。 在梯度下降法中,求某函数极大值时 ,沿着梯度方向走 ,可以最快达到极大点; 反之,沿着负梯度方向走 ,则最快地达到极小点。梯度下降法 ,就是利用负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。梯度下降法是2 范数下的最速下降法。最速下降法的一种简单形式是:x(k+1)=x(k)-a*g(k),其中 a 称为学习速率,可以是较小的常数。g(k)是 x(k)的梯度。直观的说 ,就是在一个有中心的等值线中 ,从初始值开始 ,每次沿着垂直等值线方向移动一个小的距离,最终收敛在中心。对于某一个性能指数 ,我们能够运用梯度下降法,使这个指数降到最小。若该指数为均方误差 ,我们便得到了最小均方误差(LMS)算法2 求函数 J(a)极小值的问题 ,可以选择任意初始点a0,从 a0 出发沿着负梯度方向走,可使得 J(a)下降最快。(0)0()sJ a0s:点 a0 的搜索方向。前馈控制是一种预测控制,通过对系统当前工作状态的了解,预测出下一阶段系统的运行状况。如果与参考值有偏差,那么就提前给出控制信号,使干扰获得补偿,稳定输出 ,消除误差。 前馈的缺点是在使用时需要对系统有精确的了解,只有了解了系统模型才能有针对性的给出预测补偿。但在实际工程中,并不是所有的干扰都是可测的 ,并不是所有的对象都是可得到精确模型的,而且大多数控制对象在运行的同时自身的结构也在发生变化。所以仅用前馈并不能达到良好的控制品质。这时就需要加入反馈,反馈的特点是根据偏差来决定控制输入,不管对象的模型如何 ,也不管外界的干扰如何,只要有偏差 ,就根据偏差进行纠正,可以有效的消除稳态误差。解决前馈不能控制的不可测干扰。模...