正弦定理和余弦定理专题及解析VIP免费

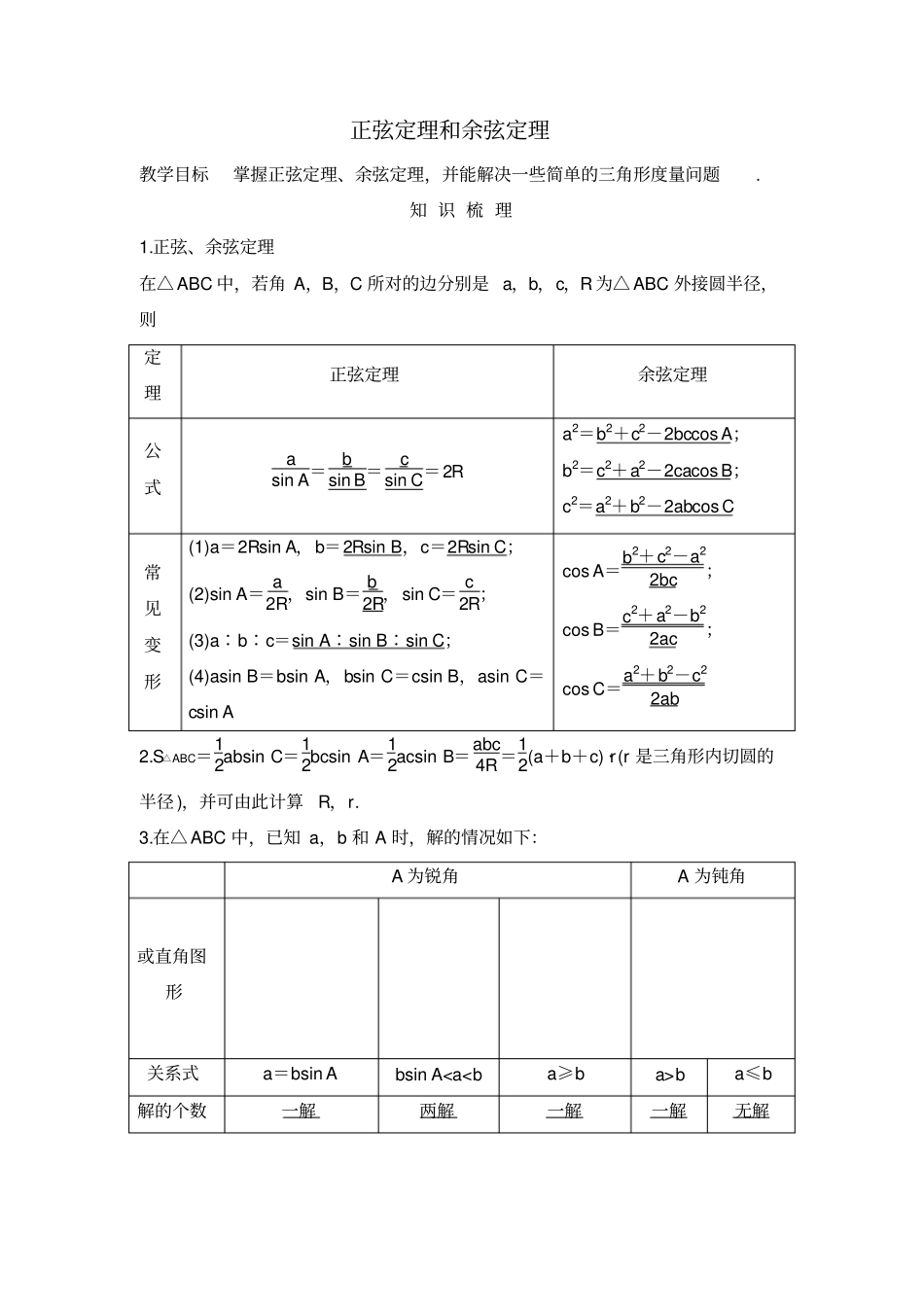
正弦定理和余弦定理教学目标掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.知 识 梳 理1.正弦、余弦定理在△ ABC 中，若角 A，B，C 所对的边分别是 a，b，c，R 为△ ABC 外接圆半径，则定理正弦定理余弦定理公式asin A＝bsin B＝csin C＝2Ra2＝b2＋c2－2bccos A；b2＝c2＋a2－2cacos B；c2＝a2＋b2－2abcos C常见变形(1)a＝2Rsin A，b＝2Rsin B，c＝2Rsin C；(2)sin A＝ a2R，sin B＝ b2R，sin C＝ c2R；(3)a∶b∶c＝sin A∶sin B∶sin C；(4)asin B＝bsin A，bsin C＝csin B，asin C＝csin Acos A＝b2＋c2－a22bc；cos B＝c2＋a2－b22ac；cos C＝a2＋b2－c22ab2.S△ABC＝12absin C＝12bcsin A＝12acsin B＝abc4R＝12(a＋b＋c) ·r(r 是三角形内切圆的半径 )，并可由此计算R，r. 3.在△ ABC 中，已知 a，b 和 A 时，解的情况如下：A 为锐角A 为钝角或直角图形关系式a＝bsin Absin Aba≤b解的个数一解两解一解一解无解诊 断 自 测1.判断正误 (在括号内打“√”或“×”)(1)三角形中三边之比等于相应的三个内角之比.()(2)在△ABC 中，若 sin A>sin B，则 A>B.()(3)在△ABC 的六个元素中，已知任意三个元素可求其他元素.()(4)当 b2＋c2－a2>0 时，△ABC 为锐角三角形；当 b2＋c2－a2＝0 时，△ABC 为直角三角形；当 b2＋c2－a2<0 时，△ ABC 为钝角三角形 .()(5)在三角形中，已知两边和一角就能求三角形的面积.()解析(1)三角形中三边之比等于相应的三个内角的正弦值之比.(3)已知三角时，不可求三边.(4)当 b2＋c2－a2>0 时，三角形 ABC 不一定为锐角三角形 .答案(1)×(2)√(3)×(4)×(5)√2.(2016 ·全国Ⅰ卷)△ABC 的内角 A，B，C 的对边分别为 a，b，c.已知 a＝5，c＝2，cos A＝23，则 b＝()A.2 B.3 C.2 D.3解析由余弦定理，得5＝b2＋22－2×b×2×23，解得 b＝3 b＝－ 13舍去 ，故选D.答案D3.(2017 ·郑州预测 )在△ ABC 中，角 A，B，C 所对的边分别为 a，b，c，若b3cos B＝asin A，则 cos B＝()A.－12B.12C.－32D.32解析由正弦定理知sin B3cos B＝sin Asin A＝1，即 tan B＝3，由 B∈(0，π )，所以 B＝π3 ，所以 cos B＝cosπ3 ＝12，故选 B.答案B4.在△ ABC 中，A＝60° ，AB＝2，且△ ABC 的面积为32 ，则 BC 的长为 ()A.32B.3 C.2 3 D.2解析因为 S＝12×AB×ACsin A＝12×...