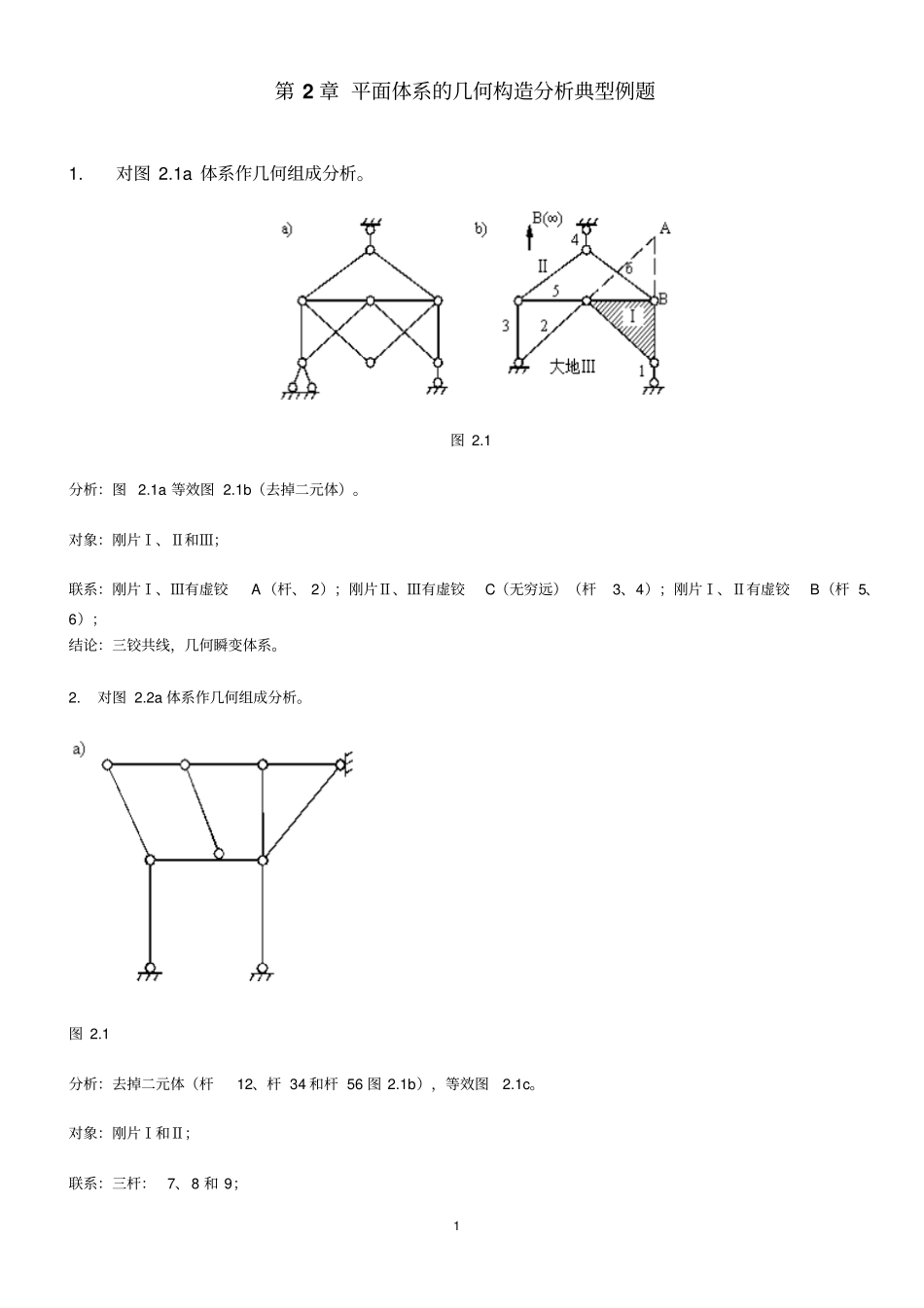
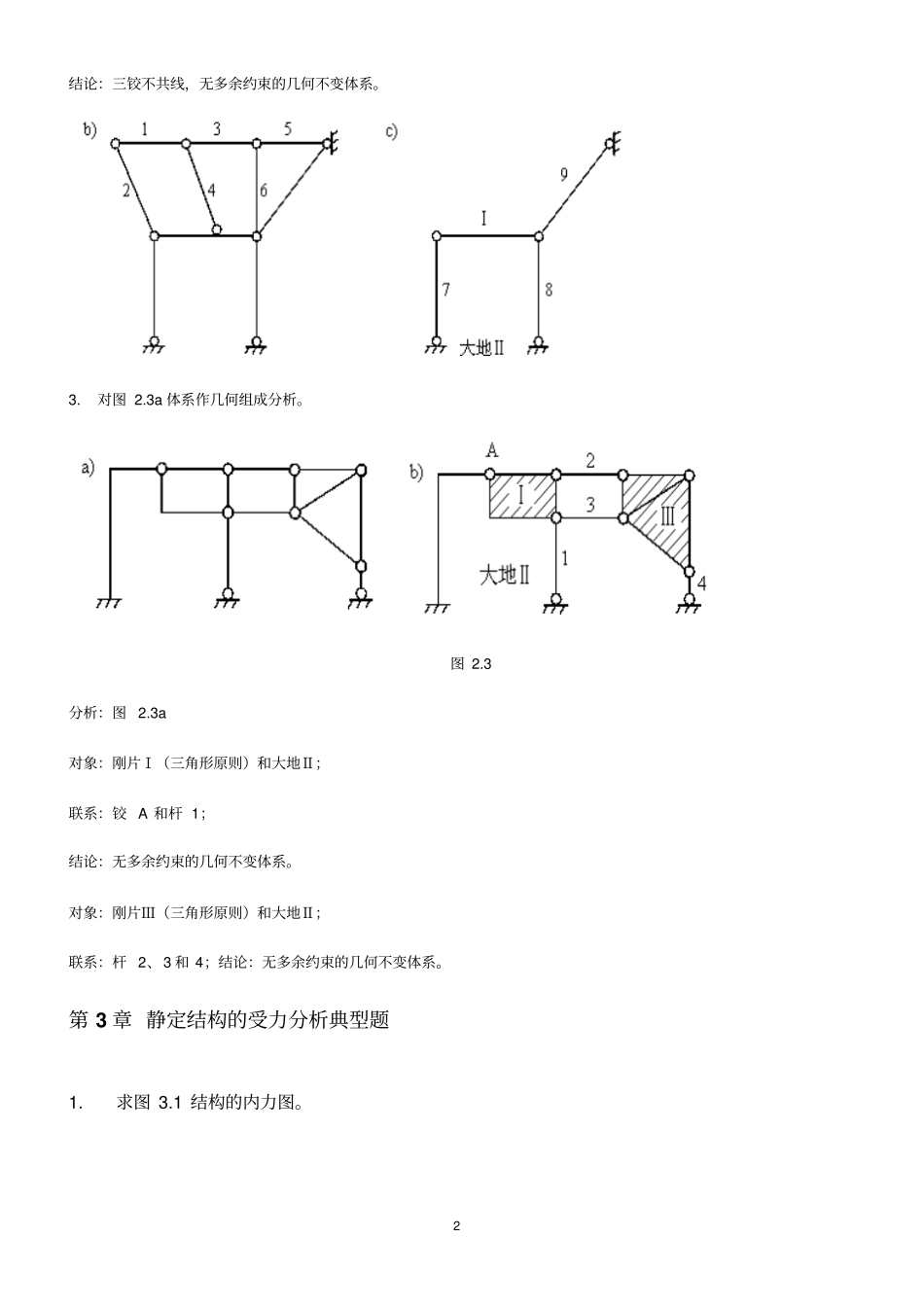
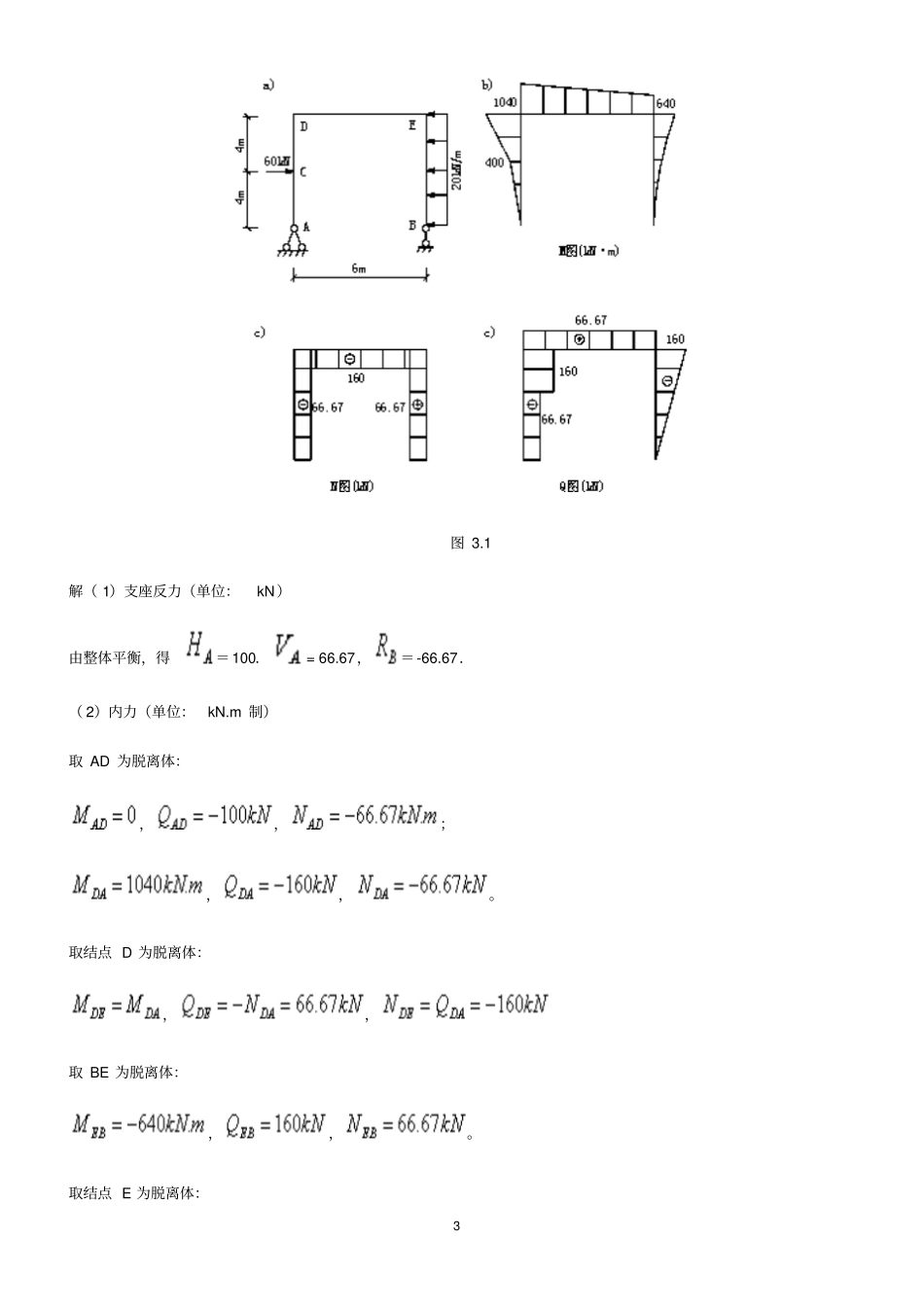
1 第 2 章 平面体系的几何构造分析典型例题1. 对图 2.1a 体系作几何组成分析。图 2.1 分析:图 2.1a 等效图 2.1b(去掉二元体)。对象:刚片Ⅰ、Ⅱ和Ⅲ;联系:刚片Ⅰ、Ⅲ有虚铰A(杆、 2);刚片Ⅱ、Ⅲ有虚铰C(无穷远)(杆3、4);刚片Ⅰ、Ⅱ有虚铰B(杆 5、6);结论:三铰共线,几何瞬变体系。2. 对图 2.2a 体系作几何组成分析。图 2.1 分析:去掉二元体(杆12、杆 34 和杆 56 图 2.1b),等效图2.1c。对象:刚片Ⅰ和Ⅱ;联系:三杆: 7、8 和 9;2 结论:三铰不共线,无多余约束的几何不变体系。3. 对图 2.3a 体系作几何组成分析。图 2.3 分析:图 2.3a 对象:刚片Ⅰ(三角形原则)和大地Ⅱ;联系:铰 A 和杆 1;结论:无多余约束的几何不变体系。对象:刚片Ⅲ(三角形原则)和大地Ⅱ;联系:杆 2、3 和 4;结论:无多余约束的几何不变体系。第 3 章 静定结构的受力分析典型题1. 求图 3.1 结构的内力图。3 图 3.1 解( 1)支座反力(单位:kN)由整体平衡,得=100.= 66.67,=-66.67.( 2)内力(单位:kN.m 制)取 AD 为脱离体:,,;,,。取结点 D 为脱离体:,,取 BE 为脱离体:,,。取结点 E 为脱离体:4 ,,( 3)内力图见图3.1b~d。2. 判断图 3.2a 和 b 桁架中的零杆。图 3.2 分析:判断桁架零杆的常用方法是找出桁架中的L 型结点和 T 型结点。如果这两种结点上无荷载作用.那么L 型纪点的两杆及 T 型结点的非共线杆均为零杆。解:图 3.2a:考察结点 C、D、E、I、 K、 L,这些结点均为T 型结点,且没有荷载作用,故杆件CG、DJ、EH、IJ、KH、 LF均为零杆。考察结点 G 和 H,这两个结点上的两竖向链杆均已判断为零杆,故这两个结点的受力也已成为T 型结点的情形. 由于没有荷载作用,故杆件AG 、BH 也为零杆。整个结构共有8 根零杆.如图3.2c 虚线所示。图 3.2b:考察结点 D,为 “K”型结点且无荷载作用,故;对称结构对称荷载(A 支座处的水平反力为零),有,故杆件 DE 和 DF 必为零杆。5 考察结点 E 和 F,由于 DE、DF 已判断为零杆.故杆件AE 、BF 也是零杆。整个结构共有四根零杆。如图3.2d 虚线所示。3. 图 3.3a 三铰拱为抛物线型,轴线方程为,试求截面K 的内力。图 3.3 分析:结构为一主附结构:三铰拱ACB 为基本部分, CD 和 CE 分别为附属部分。内力分析时先求出附属部分在铰C 处的反力...