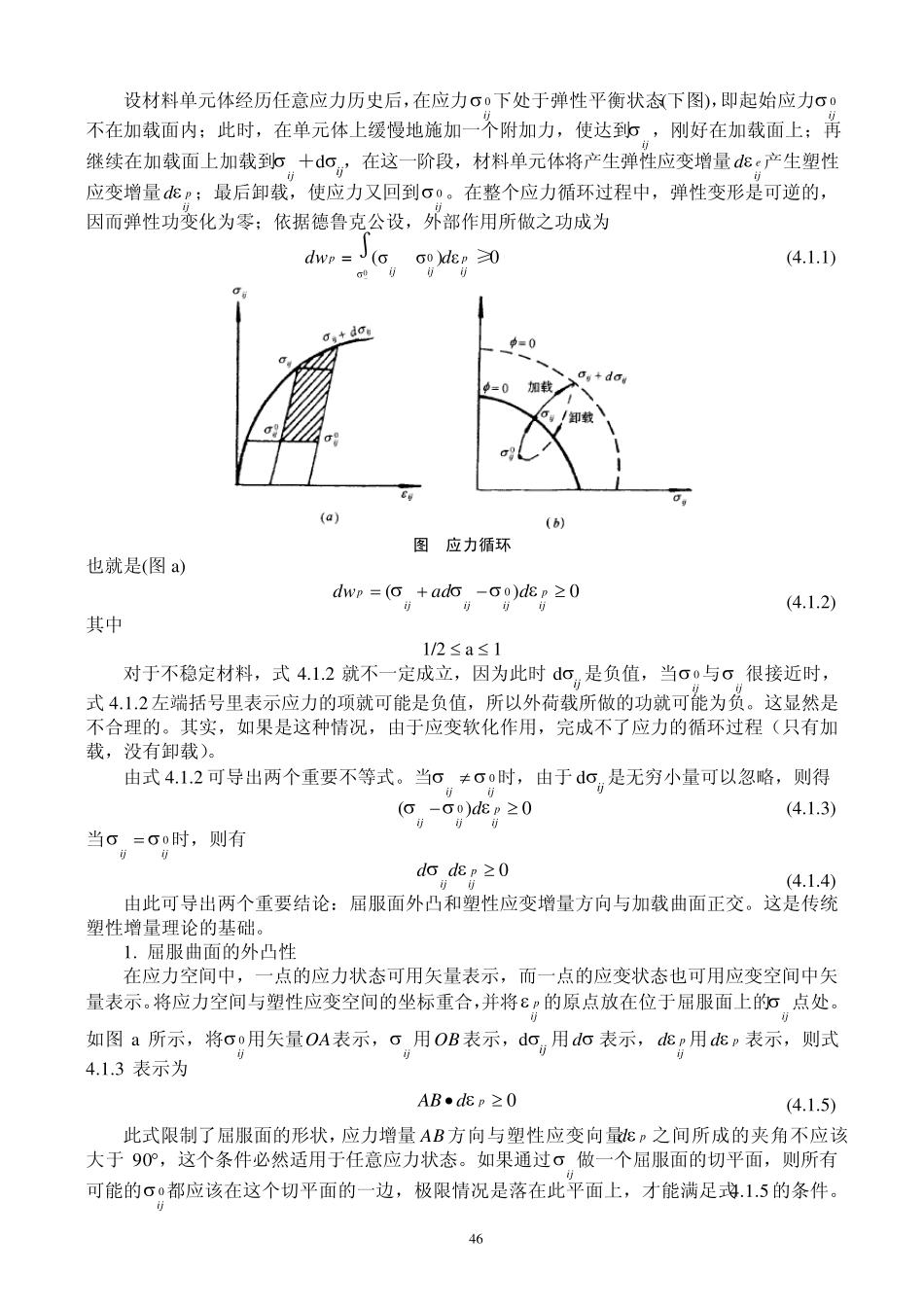
45 第四章 塑性位势理论 位势理论作为一种力学方法在弹性力学和塑性力学中都得到了广泛应用。米赛斯于1928年借用弹性势函数作为塑性势函数,并提出了按照塑性势函数的梯度方向确定塑性流动方向的传统塑性位势理论。后来又由德鲁克塑性公设,表明塑性势函数与屈服函数是一致的,从而形成了塑性应变增量方向必定正交于屈服面的关联流动法则,完善了传统塑性位势理论。传统塑性位势理论不适应岩土材料的变形机制,因而基于传统塑性位势理论而建立的岩土本构模型,不能反映岩土的实际变形。双屈服面模型与多重屈服面模型的出现实质上已经扩展了塑性位势理论。作者在研究多重屈服面弹塑性理论时,提出建立岩土本构模型应采用三个塑性势面和三个屈服面,并建立了以三个主应力作为塑性势函数的岩土本构模型。此后,杨光华用张量定律从理论上导出以三个塑性势函数表述的塑性应变增量公式。作者在剖析传统塑性位势理论的基础上,提出以三个塑性势函数表述的塑性应变增量公式,可作为不考虑应力主轴旋转时的广义塑性位势理论。并从基本力学概念出发,指出屈服函数与势函数必须相应,而不要求相等,相等只适用于金属情况。郑颖人等又进一步发展建立了考虑应力主轴旋转情况下的广义塑性位势理论。 §4.1 德鲁克(Drucker)塑性公设与伊留辛(Ильющин)塑性公设 一、 稳定与不稳定材料 下图 示出两类试验曲线。在图 a 中,当 > 0 时, >0,这时附加应力 对附加应变做功为非负,即有 > 0。这种材料被德鲁克(Dru cker)称为稳定材料。显然,应变硬化和理想塑性的材料属于稳定材料。在图 b 所示的试验曲线上,当应力点超过 p 点以后,附加应力 < 0,而附加应变 > 0,故附加应力对附加应变做负功,即 <0。这类材料称为不稳定材料,应变软化材料属于不稳定材料。 图 稳定与不稳定材料 (a)稳定材料;(b)不稳定材料 应当说明,德鲁克公设对稳定材料的定义只是充分条件,而非必要条件。因而,除了上述形式的不稳定材料外,还有其他形式的不稳定材料存在。 二、 德鲁克(Drucker)塑性公设 德鲁克公设可陈述为:对于处在某一状态下的稳定材料的质点(试件),借助于一个外部作用,在其原有应力状态之上,缓慢地施加并卸除一组附加应力,在附加应力的施加和卸除循环内,外部作用所作之功是非负的。 46 设材料单元体经历任意应力历史后,在应力0ij 下处于弹性平衡状态(下图),即起始应力...