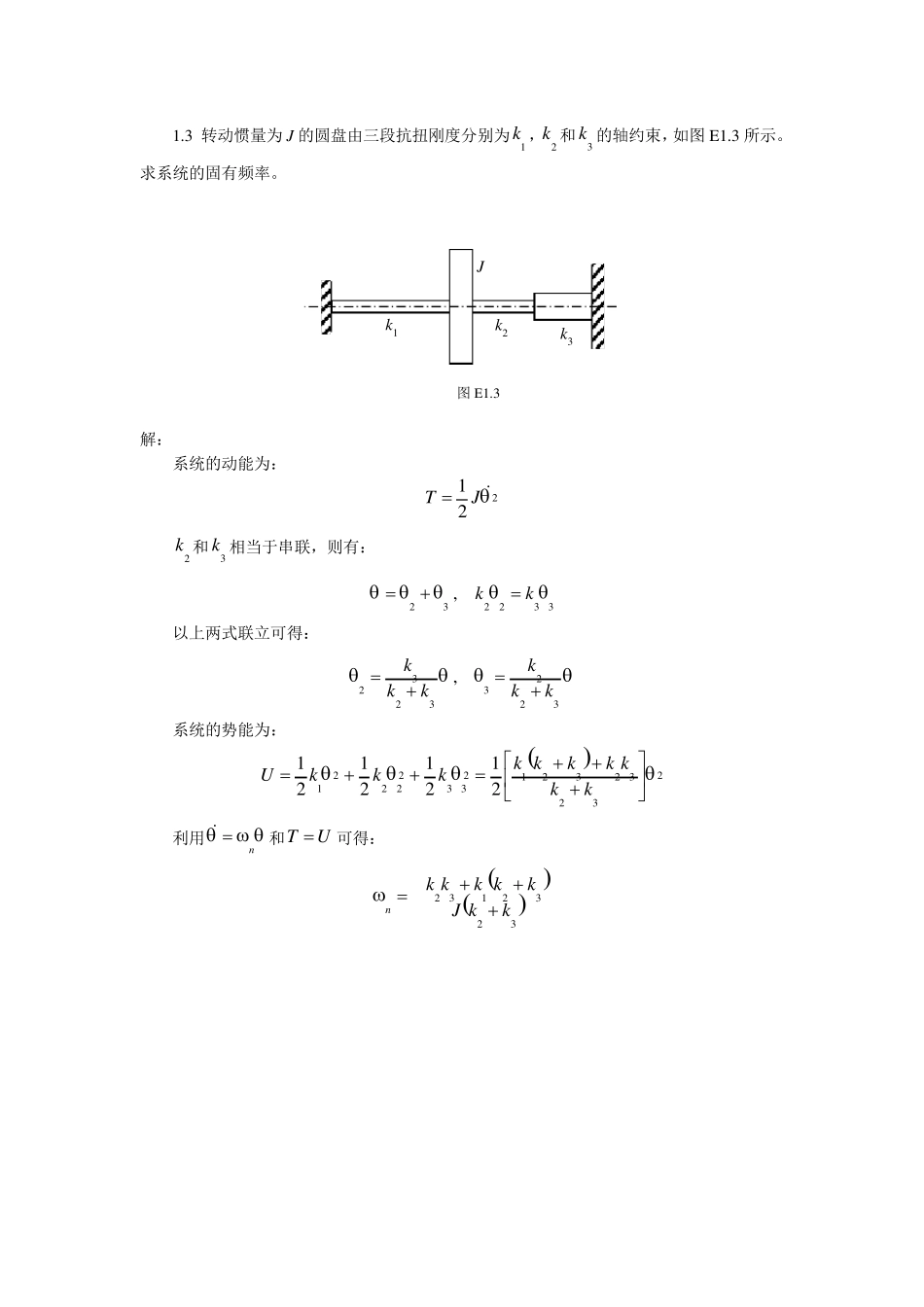
《振动力学》习题集(含答案) 1.1 质量为m 的质点由长度为l、质量为m1 的均质细杆约束在铅锤平面内作微幅摆动,如图 E1.1 所示。求系统的固有频率。 图 E1.1 解: 系统的动能为: 222121xIlxmT 其中 I 为杆关于铰点的转动惯量: 2102120131lmdxxlmxdxlmIll 则有: 221221223616121xlmmxlmxmlT 系统的势能为: 2121212414121 cos12cos1glxmmglxmmglxxlgmxmglU 利用xxn和UT 可得: lmmgmmn113223 m l m1 x 1.2 质量为m、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在 CA=a 的 A 点系有两根弹性刚度系数为k 的水平弹簧,如图 E1.2 所示。求系统的固有频率。 图 E1.2 解: 如图,令 为柱体的转角,则系统的动能和势能分别为: 22222243212121mRmRmRITB 222212aRkaRkU 利用n和UT 可得: mkRaRmRaRkn343422 k k A C a R 1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3 所示。求系统的固有频率。 图E1.3 解: 系统的动能为: 221 JT 2k 和3k 相当于串联,则有: 332232 , kk 以上两式联立可得: 32233232 , kkkkkk 系统的势能为: 232323212332222121212121kkkkkkkkkkU 利用n和UT 可得: 3232132kkJkkkkkn k1 k2 k3 J 1.4 在图E1.4 所示的系统中,已知bamiki , ,3,2,1 和,横杆质量不计。求固有频率。 图E1.4 答案图E1.4 解: 对 m 进行受力分析可得: 33xkmg ,即33kmgx 如图可得: 22221111 ,kbamgakFxkbamgbkFx mgkkbakbkabaxxaxxxx212221212110 mgkmgkkkbakbkaxxx0321222123011 则等效弹簧刚度为: 2123223123212kkbakkbkkakkkbake 则固有频率为: 222132212321bkakkbakkmbakkkmken mgbaaF2 mg a b x1 x2 x0 x mgbabF1 k2 k1 a b k3 m 1.7 质量1m 在倾角为 的光滑斜面上从高h 处滑下无...