《数字信号处理》课后上机题VIP免费

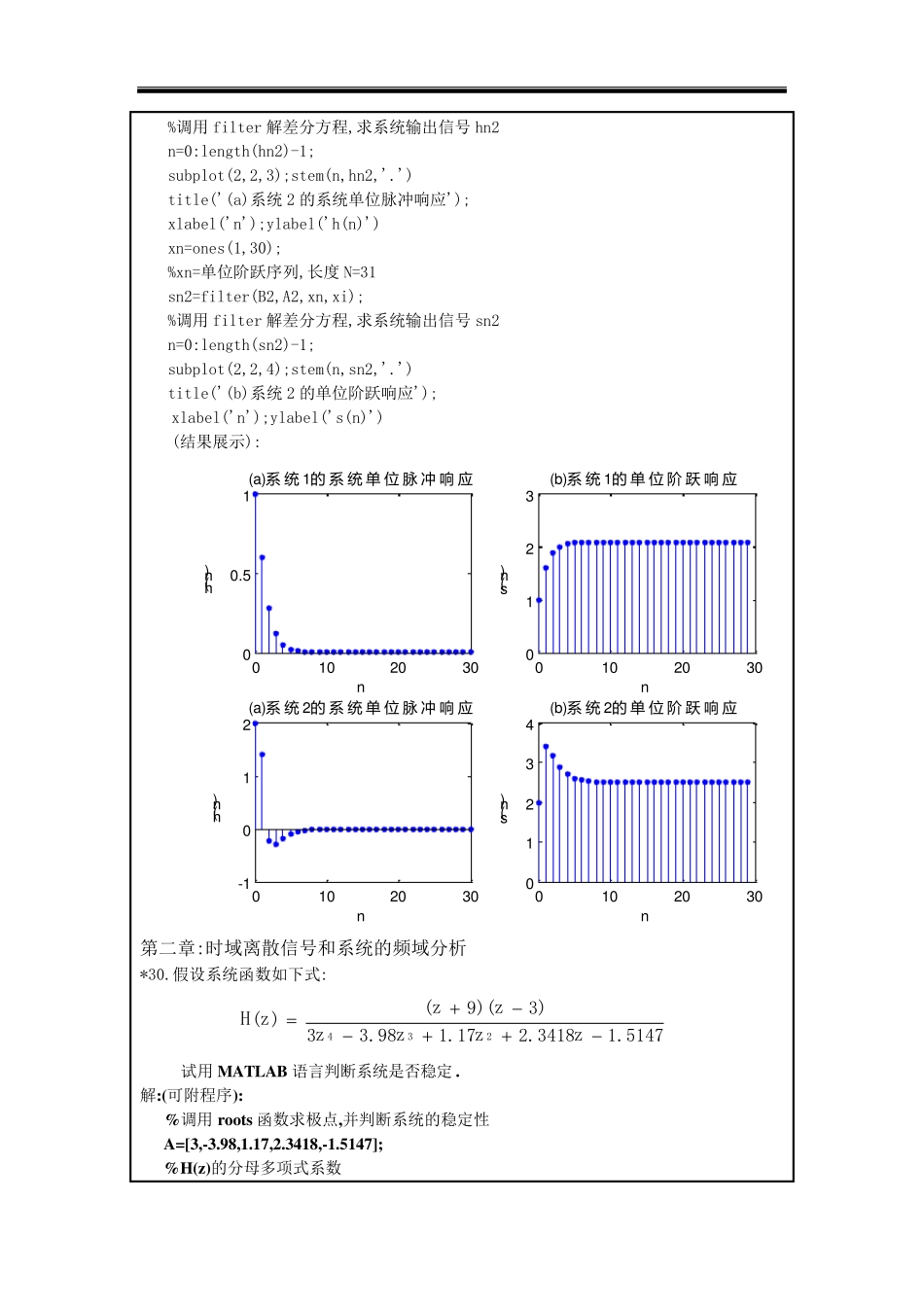
实验报告 第一章:时域离散信号和时域离散系统 *16.已知两个系统的差分方程分别为 (1) y(n)=0.6y(n-1)-0.08y(n-2)+x(n) (2) y(n)=0.7y(n-1)-0.1y(n-2)+2x(n)-x(n-2) 分别求出所描述的系统的单位脉冲响应和单位阶跃响应. 解:(可附程序) (1) 系统差分方程的系数向量为 B1=1,A1=[1,-0.6,0.08] (2) 系统差分方程的系数向量为 B2=[2,0,-1],A2=[1,-0.7,0.1] 调用 MATLAB 函数 filter 计算两个系统的单位脉冲响应和单位阶跃响应的程序%B1=1;A1=[1,-0.6,0.08]; %设差分方程(1)系数向量 B2=[2,0,-1];A2=[1,-0.7,0.1]; %设差分方程(2)系数向量 %系统 1 xn=[1,zeros(1,30)]; ys=0; %xn=单位脉冲序列,长度 N=31 xi=filtic(B1,A1,ys); %由初始条件计算等效初始条件输入序列 xi hn1=filter(B1,A1,xn,xi); %调用 filter 解差分方程,求系统输出信号 hn1 n=0:length(hn1)-1; subplot(2,2,1);stem(n,hn1,'.') title('(a)系统 1 的系统单位脉冲响应'); xlabel('n');ylabel('h(n)') xn=ones(1,30); %xn=单位阶跃序列,长度 N=31 sn1=filter(B1,A1,xn,xi); %调用 filter 解差分方程,求系统输出信号 sn1 n=0:length(sn1)-1; subplot(2,2,2);stem(n,sn1,'.') title('(b)系统 1 的单位阶跃响应'); xlabel('n');ylabel('s(n)') %系统 2 xn=[1,zeros(1,30)]; %xn=单位脉冲序列,长度 N=31 xi=filtic(B2,A2,ys); %由初始条件计算等效初始条件输入序列 xi hn2=filter(B2,A2,xn,xi); %调用filter 解差分方程,求系统输出信号hn2 n=0:length(hn2)-1; subplot(2,2,3);stem(n,hn2,'.') title('(a)系统2 的系统单位脉冲响应'); xlabel('n');ylabel('h(n)') xn=ones(1,30); %xn=单位阶跃序列,长度N=31 sn2=filter(B2,A2,xn,xi); %调用filter 解差分方程,求系统输出信号sn2 n=0:length(sn2)-1; subplot(2,2,4);stem(n,sn2,'.') title('(b)系统2 的单位阶跃响应'); xlabel('n');ylabel('s(n)') (结果展示): 010203000.51(a)系 统 1的 系 统 单 位 脉 冲 响 应nh(n)01020300123(b)系 统 1的 单 位 阶 跃 响 应ns(n)0102030-1012(a)系 统 2的 系 统 单 位 脉 冲 响 应nh(n)010203001234(b)系 统 2的 单 位 阶 跃 响 应ns(n)第二章:时域离散信号和系统的频域分析 *30.假设系统函数如下式: 5147.13418.217.198.33)3)(9()(234zzzzzzzH 试用MATLAB ...