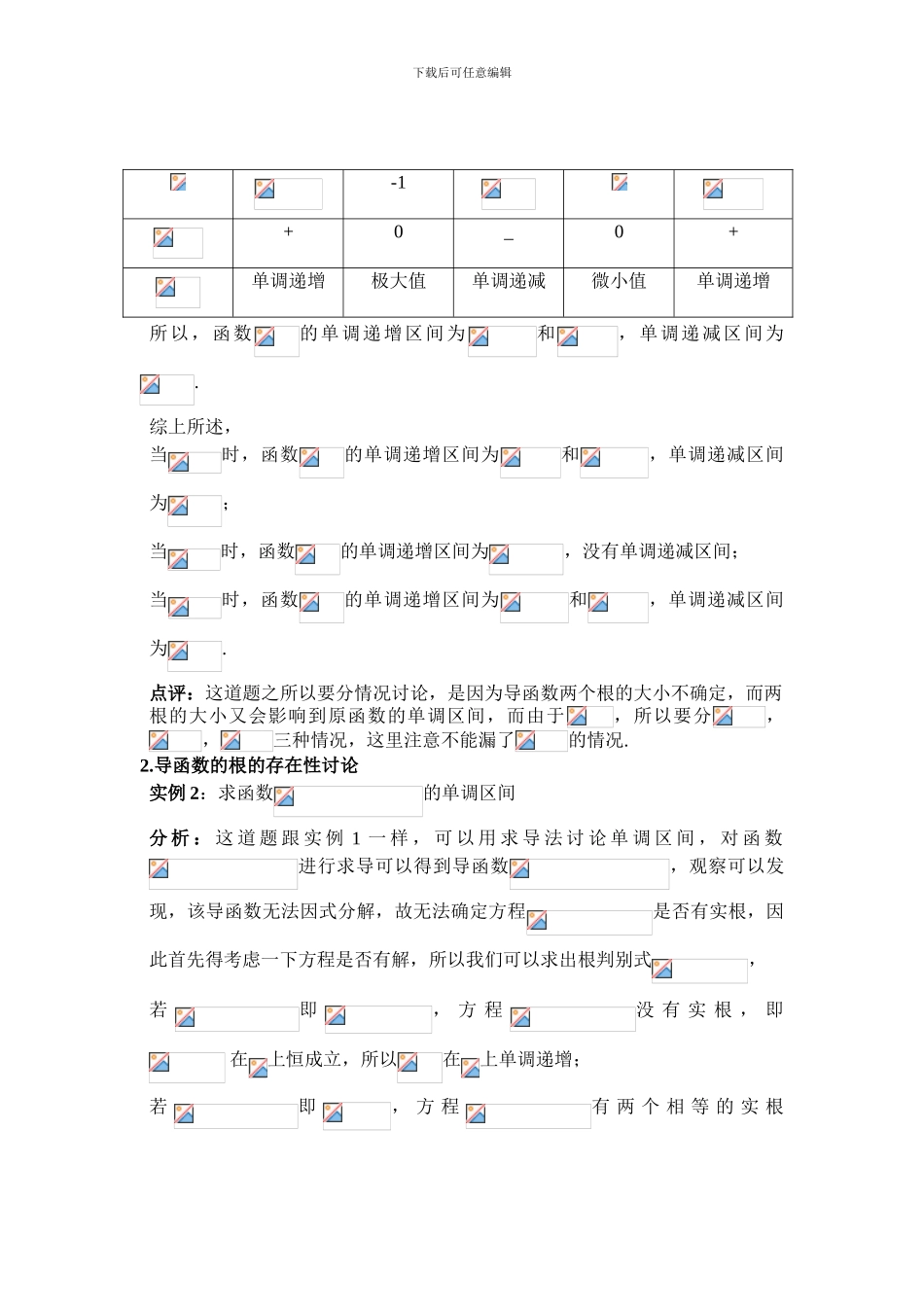
下载后可任意编辑导数中分类讨论的三种常见类型高中数学中,分类讨论思想是解决含有参数的复杂数学问题的重要途径,而所谓分类讨论,就是当问题所给的讨论对象不能进行统一的讨论处理时,对讨论对象根据某种标准进行分类,然后对每一类的对象进行分别的讨论并得出结论,最后综合各类的讨论结果对问题进行整体的解释.几乎所有的高中生都对分类讨论思想有所了解,而能正确运用分类讨论思想解决问题的不到一半,不能运用分类讨论思想解决具体问题的主要原因是对于一个复杂的数学问题不知道该不该去分类以及如何进行合理的分类,下面根据导数中 3 种比较常见的分类讨论类型谈谈导数中如何把握对参数的分类讨论.1.导函数根的大小比较实例 1:求函数,的单调区间.分析:对于三次或三次以上的函数求单调区间,基本上都是用求导法,所以对函 数进 行 求 导 可 以 得 到 导 函 数, 观 察 可 知 导 函 数 可 以 因 式 分 解 为, 由 此 可 知 方 程有 两 个 实 根,,由于的范围未知,要讨论函数的单调性,需要讨论两个根的大小,所以这里分,,三种情况进行讨论:当时,,随的变化情况如下: -1+0_0+单调递增极大值单调递减微小值单调递增所以,函数的单调递增区间为和,单调递减区间为.当时, 在上恒成立,所以函数的单调递增区间为,没有单调递减区间.当时,,随的变化情况如下:下载后可任意编辑-1+0_0+单调递增极大值单调递减微小值单调递增所以,函数的单调递增区间为和,单调递减区间为.综上所述,当时,函数的单调递增区间为和,单调递减区间为;当时,函数的单调递增区间为,没有单调递减区间;当时,函数的单调递增区间为和,单调递减区间为.点评:这道题之所以要分情况讨论,是因为导函数两个根的大小不确定,而两根的大小又会影响到原函数的单调区间,而由于,所以要分,,三种情况,这里注意不能漏了的情况.2.导函数的根的存在性讨论实例 2:求函数的单调区间分 析 : 这 道 题 跟 实 例 1 一 样 , 可 以 用 求 导 法 讨 论 单 调 区 间 , 对 函 数进行求导可以得到导函数,观察可以发现,该导函数无法因式分解,故无法确定方程是否有实根,因此首先得考虑一下方程是否有解,所以我们可以求出根判别式,若即, 方 程没 有 实 根 , 即 在上恒成立,所以在上单调递增;若即, 方 程有 两 个 相 等 的 实 根下载后可任意编辑,即在上恒成立,所以在上...