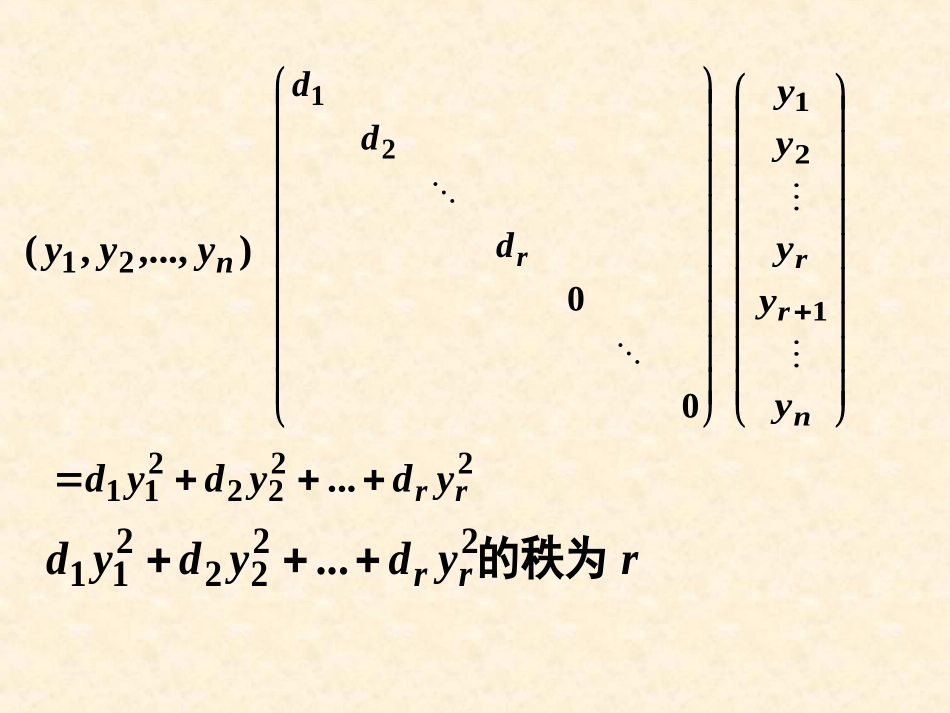二次型的标准型与规范型VIP免费

第二节第二节标准形的定义标准形的定义正交线性替换法正交线性替换法配方法配方法二次型的标准形与规范形二次型的标准形与规范形初等变换法初等变换法二次型的规范形二次型的规范形一、标准形的定义一、标准形的定义定义定义二次型二次型ff((xx11,,xx22,…,,…,xxnn))经过非退经过非退化化线性替换线性替换x=Cyx=Cy所变成的如下形式所变成的如下形式((只含平方只含平方项项))yyTTBy=dBy=d11yy1122++dd22yy2222+…++…+ddrryyrr22((rrnn)(4.5))(4.5)的二次型称为二次型的二次型称为二次型ff((xx11,,xx22,…,,…,xxnn))的的标准标准形形..不难看出，二次型(4.5)的矩阵B为n阶对角矩阵.即B=CTAC=diag(d1,d2,…,dr,0,…,0).0021rddd),...,,(21nyyynrryyyyy1212222211...rrydydydrydydydrr的秩为2222211...二、用正交线性替换法二、用正交线性替换法化二次型为标准形化二次型为标准形任一任一((实实))二次型一定可以通过正交线性替换二次型一定可以通过正交线性替换化为标准形化为标准形...,,,,,2.4212222211的全部特征值是二次型的矩阵其中把它化为标准形使得经过正交替换一定存在正交矩阵对于二次型定理AyyyQyxQXAXnnnT.,,14.31为对角阵使得正交矩阵且存在一定与对角矩阵相似实对称矩阵定理AQQQA例例11用正交线性替换化下列二次型为标准形,并求出所作的正交线性替换:;222)(323121321xxxxxx,x,xxf111111A|E|,)1)(2(2.1113p,21101121p,p,01121111ppe,21161222ppe.11131333ppe一般地，用正交线性替换将二次型f(x1,x2,…,xn)=xTAx(其中AT=A)化为标准形的步骤如下:Step1Step1求出二次型矩阵A的全部特征值1,2,…,n;Step2Step2求出正交矩阵P，使PTAP=diag(1,2,…,n);Step3Step3作正交线性替换X=PY，其中Y=(x1,x2,…,xn)TRn，则二次型f(x1,x2,…,xn)化为标准形1y12+2y22+…+nyn2.三、用配方法三、用配方法化二次型为标准形化二次型为标准形例例22用配方法把三元二次型32312123222132184432),,(xxxxxxxxxxxxf化为标准形，并求所用的线性替换及变换矩阵.例例33用配方法化二次型323121321622),,(xxxxxxxxxf为标准形.即任何一个对称矩阵都与一个对角矩阵合同.,A对任意对称矩阵为对角矩阵使得矩阵ACCT,C存在可逆矩阵即为对角矩阵使都存在一个可逆矩阵对任意对称矩阵定理,,,'3.4ACCCAT线性替换化为标准形每个二次型都可经可逆定理3.4,AxxT对任意二次型为标准形使得yACCyTT)(,Cyx存在可逆线性替换四、用初等变换法四、用初等变换法化二次型为标准形化二次型为标准形EA对对AA施以一系施以一系列行初等变换列行初等变换对对EA施以一系列施以一系列同种列初等变换同种列初等变换PsT…P2TP1TAP1P2…PsP1P2…Ps3231212322218241212312xxxxxxxxxf例例44用初等变换法化二次型为标准形.例例55用初等变换法化二次型323121321622),,(xxxxxxxxxf为标准形.五、二次型的规范形五、二次型的规范形标准形唯一吗？标准形不唯一!323121321622),,(xxxxxxxxxf如果二次型f(x1,x2,…,xn)=xTAx(其中AT=A)通过可逆线性替换可以化为yy1122+…++…+yypp22––yy22pp+1+1–…––…–yyrr22((pprrnn))则称上式为该二次型的规范形规范形..规范形中,正项的个数p称为二次型的正惯性指标正惯性指标,负项个数r－p称为二次型的负惯性指标负惯性指标.r是二次型的秩.p–(r–p)=2p–r称为二次型的符号差符号差定理定理4.44.4任一二次型任一二次型ff((xx11,,xx22,,…,…,xnxn))都可以通过可逆线性替换化为规范形，且规都可以通过可逆线性替换化为规范形，且规范形是唯一的范形是唯一的..推论1任一实对称矩阵A都与对角矩阵合同,其中1和－1的个数共有r个,r为二次型的秩.OEEprp推论2两个实对称矩阵合同的充分必要条件是它们具有相同的正惯指数和秩.则它的规范形为秩为的正惯性指数为如果二次型例,4,2),,,,(.54321xxxxxf24232221yyyy