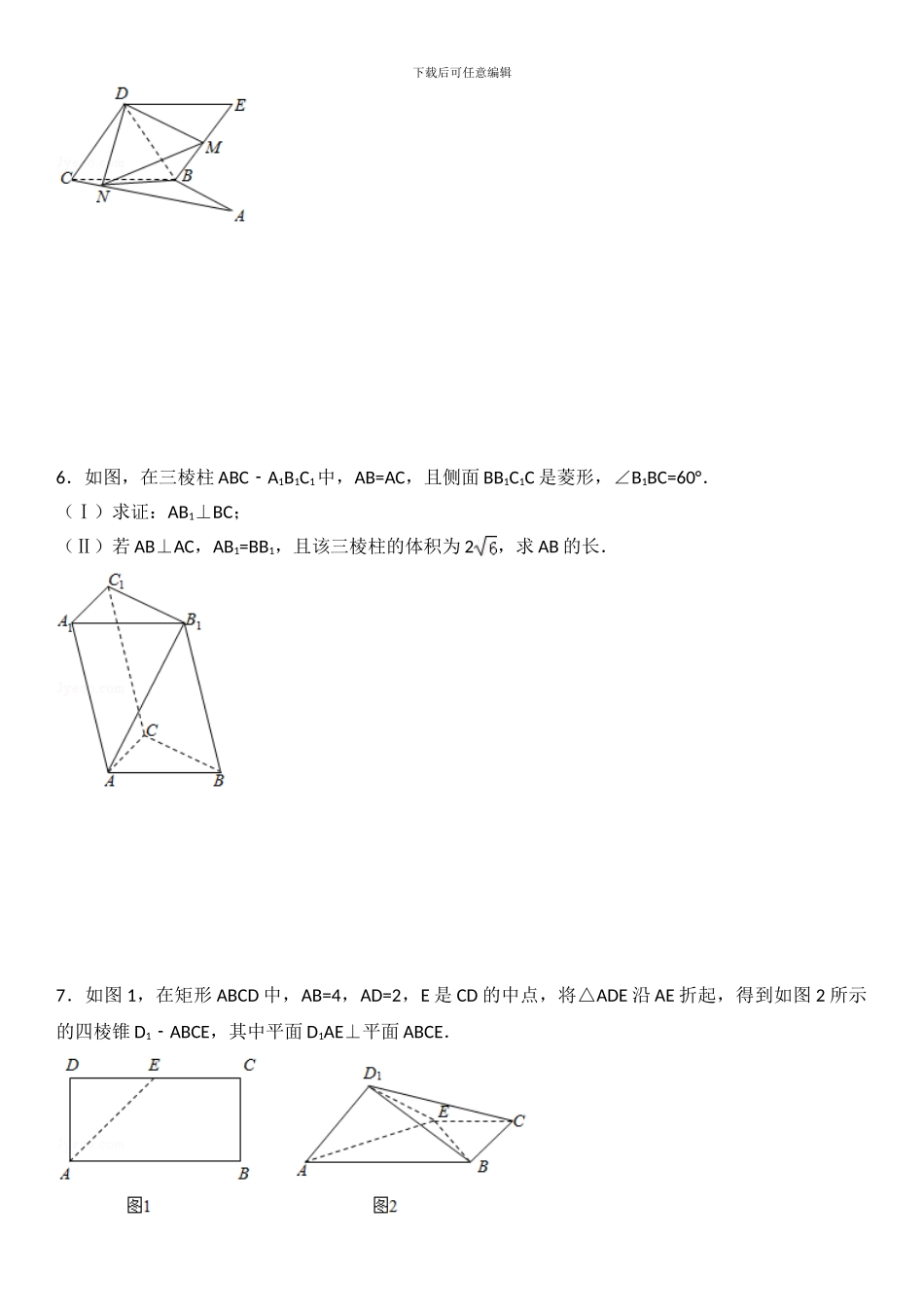
下载后可任意编辑文科立体几何大题复习 一.解答题(共 12 小题)1.如图 1,在正方形 ABCD 中,点,E,F 分别是 AB,BC 的中点,BD 与 EF 交于点 H,点 G,R 分别在线段 DH,HB 上,且.将△AED,△CFD,△BEF 分别沿 DE,DF,EF 折起,使点 A,B,C重合于点 P,如图 2 所示.(1)求证:GR⊥平面 PEF;(2)若正方形 ABCD 的边长为 4,求三棱锥 PDEF﹣的内切球的半径.2.如图,在四棱锥 PABCD﹣中,PD⊥平面 ABCD,底面 ABCD 是菱形,∠BAD=60°,AB=2,PD=,O 为 AC 与 BD 的交点,E 为棱 PB 上一点.(Ⅰ)证明:平面 EAC⊥平面 PBD;(Ⅱ)若 PD∥平面 EAC,求三棱锥 PEAD﹣的体积.3.如图,在四棱锥中 PABCD﹣,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD 是正三角形.(1)求证:AD⊥PB;下载后可任意编辑(2)已知点 M 是线段 PC 上,MC=λPM,且 PA∥平面 MQB,求实数 λ 的值.4.如图,四棱锥 SABCD﹣的底面是正方形,每条侧棱的长都是底面边长的倍,P 为侧棱 SD 上的点.(Ⅰ)求证:AC⊥SD;(Ⅱ)若 SD⊥平面 PAC,则侧棱 SC 上是否存在一点 E,使得 BE∥平面 PAC.若存在,求 SE:EC 的值;若不存在,试说明理由.5.如图所示,△ABC 所在的平面与菱形 BCDE 所在的平面垂直,且 AB⊥BC,AB=BC=2,∠BCD=60°,点 M 为 BE 的中点,点 N 在线段 AC 上.(Ⅰ)若=λ,且 DN⊥AC,求 λ 的值;(Ⅱ)在(Ⅰ)的条件下,求三棱锥 BDMN﹣的体积.下载后可任意编辑6.如图,在三棱柱 ABCA﹣1B1C1中,AB=AC,且侧面 BB1C1C 是菱形,∠B1BC=60°.(Ⅰ)求证:AB1⊥BC;(Ⅱ)若 AB⊥AC,AB1=BB1,且该三棱柱的体积为 2,求 AB 的长.7.如图 1,在矩形 ABCD 中,AB=4,AD=2,E 是 CD 的中点,将△ADE 沿 AE 折起,得到如图 2 所示的四棱锥 D1ABCE﹣,其中平面 D1AE⊥平面 ABCE.下载后可任意编辑(1)证明:BE⊥平面 D1AE;(2)设 F 为 CD1的中点,在线段 AB 上是否存在一点 M,使得 MF∥平面 D1AE,若存在,求出的值;若不存在,请说明理由.8 . 如 图 , 已 知 多 面 体 ABCDEF 中 , △ ABD 、 △ ADE 均 为 正 三 角 形 , 平 面 ADE⊥ 平 面ABCD,AB∥CD∥EF,AD:EF:CD=2:3:4.(Ⅰ)求证:BD⊥平面 BFC;(Ⅱ)若 AD=2,求该多面体的体积.9.如图,在四棱锥中 PABCD﹣,...