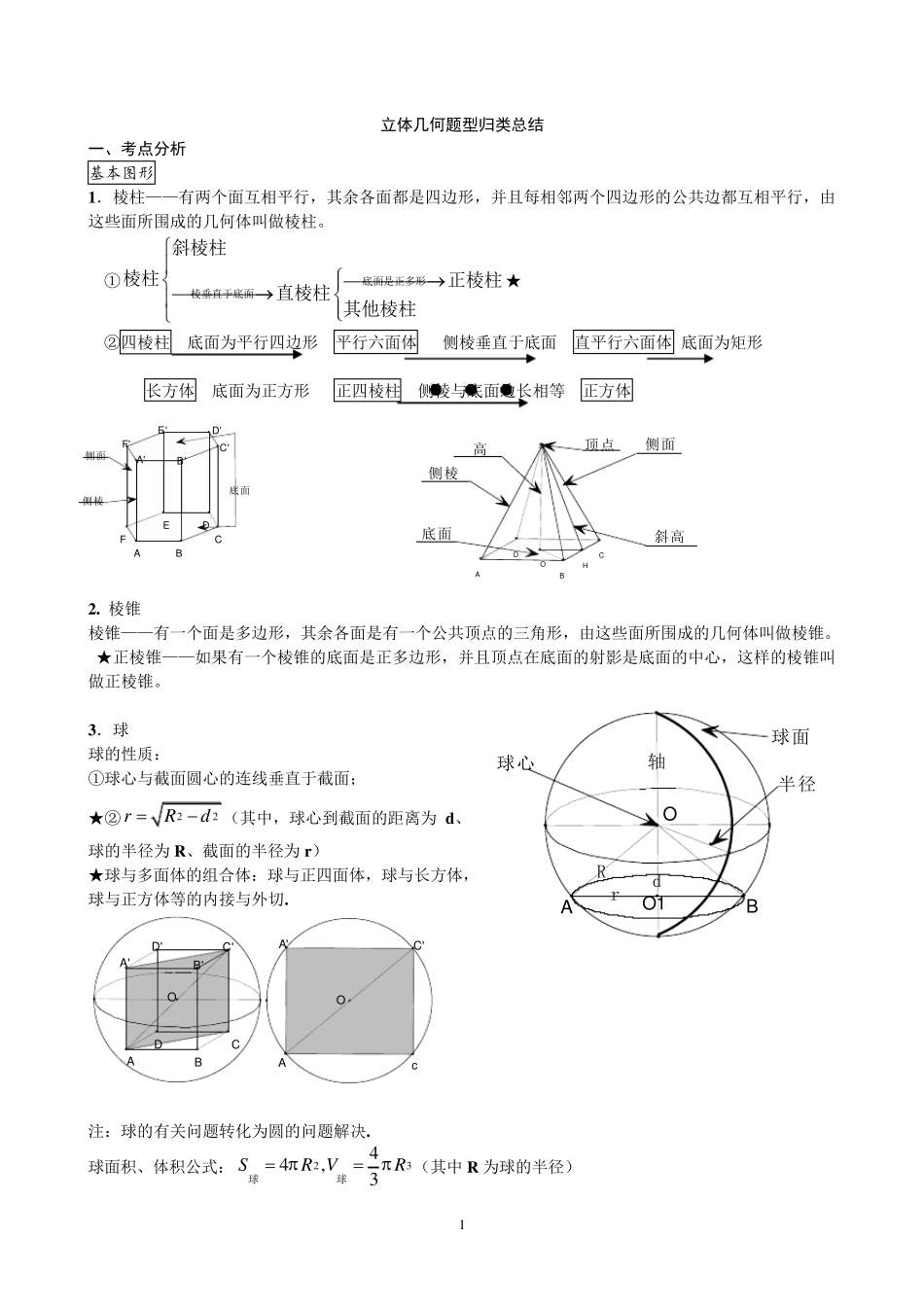
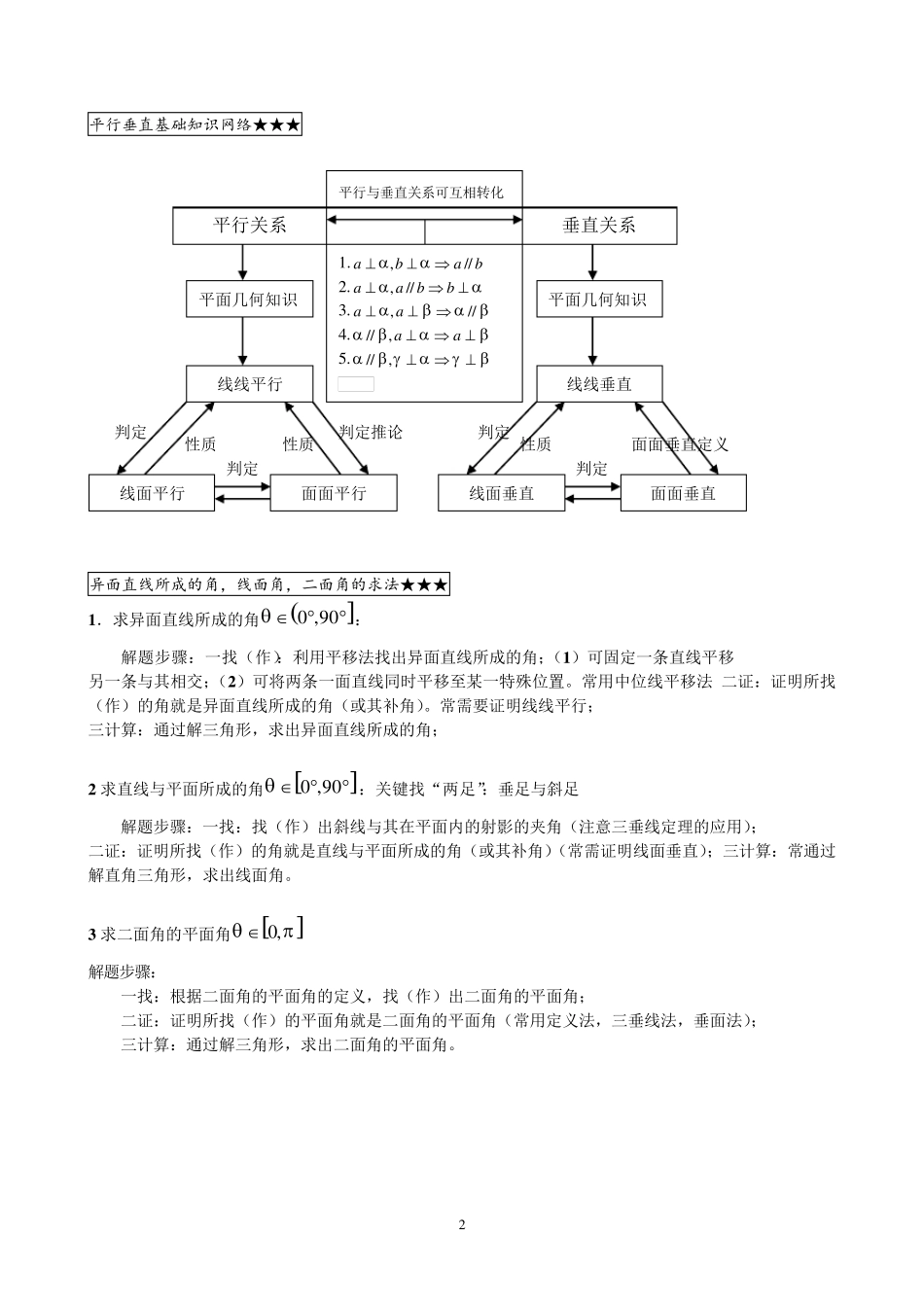
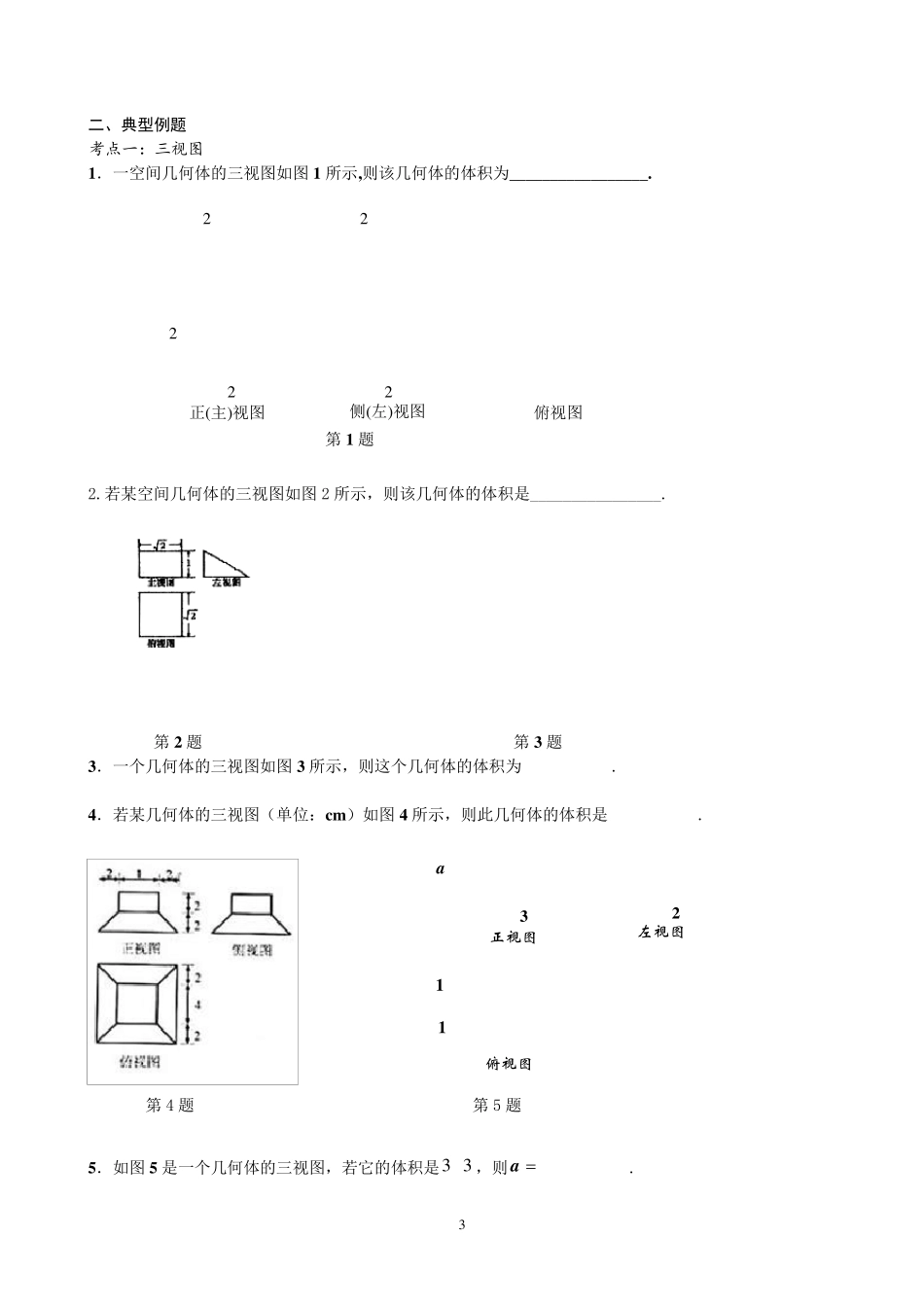
1 立体几何题型归类总结 一、考点分析 基本图形 1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。 ①底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱★ ②四棱柱 底面为平行四边形 平行六面体 侧棱垂直于底面 直平行六面体 底面为矩形 长方体 底面为正方形 正四棱柱 侧棱与底面边长相等 正方体 2. 棱锥 棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。 ★正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。 3.球 球的性质: ①球心与截面圆心的连线垂直于截面; ★②22rRd(其中,球心到截面的距离为 d、球的半径为 R、截面的半径为 r) ★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切. 注:球的有关问题转化为圆的问题解决. 球面积、体积公式:2344,3SR VR球球(其中 R 为球的半径) 顶点侧面斜高高侧棱底面OCDABHS侧棱侧面底面E'B'D'C'A'F'BDEAFCrdR球面轴球心半径AOO1BA'C'D'B'CDOABOC'A'Ac 2 平行垂直基础知识网络★★★ 异面直线所成的角,线面角,二面角的求法★★★ 1 .求异面直线所成的角0 ,9 0 : 解题步骤:一找(作):利用平移法找出异面直线所成的角;(1 )可固定一条直线平移 另一条与其相交;(2 )可将两条一面直线同时平移至某一特殊位置。常用中位线平移法 二证:证明所找(作)的角就是异面直线所成的角(或其补角)。常需要证明线线平行; 三计算:通过解三角形,求出异面直线所成的角; 2 求直线与平面所成的角0 ,9 0 :关键找“两足”:垂足与斜足 解题步骤:一找:找(作)出斜线与其在平面内的射影的夹角(注意三垂线定理的应用); 二证:证明所找(作)的角就是直线与平面所成的角(或其补角)(常需证明线面垂直);三计算:常通过解直角三角形,求出线面角。 3 求二面角的平面角0 , 解题步骤: 一找:根据二面角的平面角的定义,找(作)出二面角的平面角; 二证:证明所找(作)的平面角就是二面角的平面角(常用定义法,三垂线法,垂面法); 三计算:通过解三角形,求出二面角的平面角。 平行关系 平面几何知识 线线...