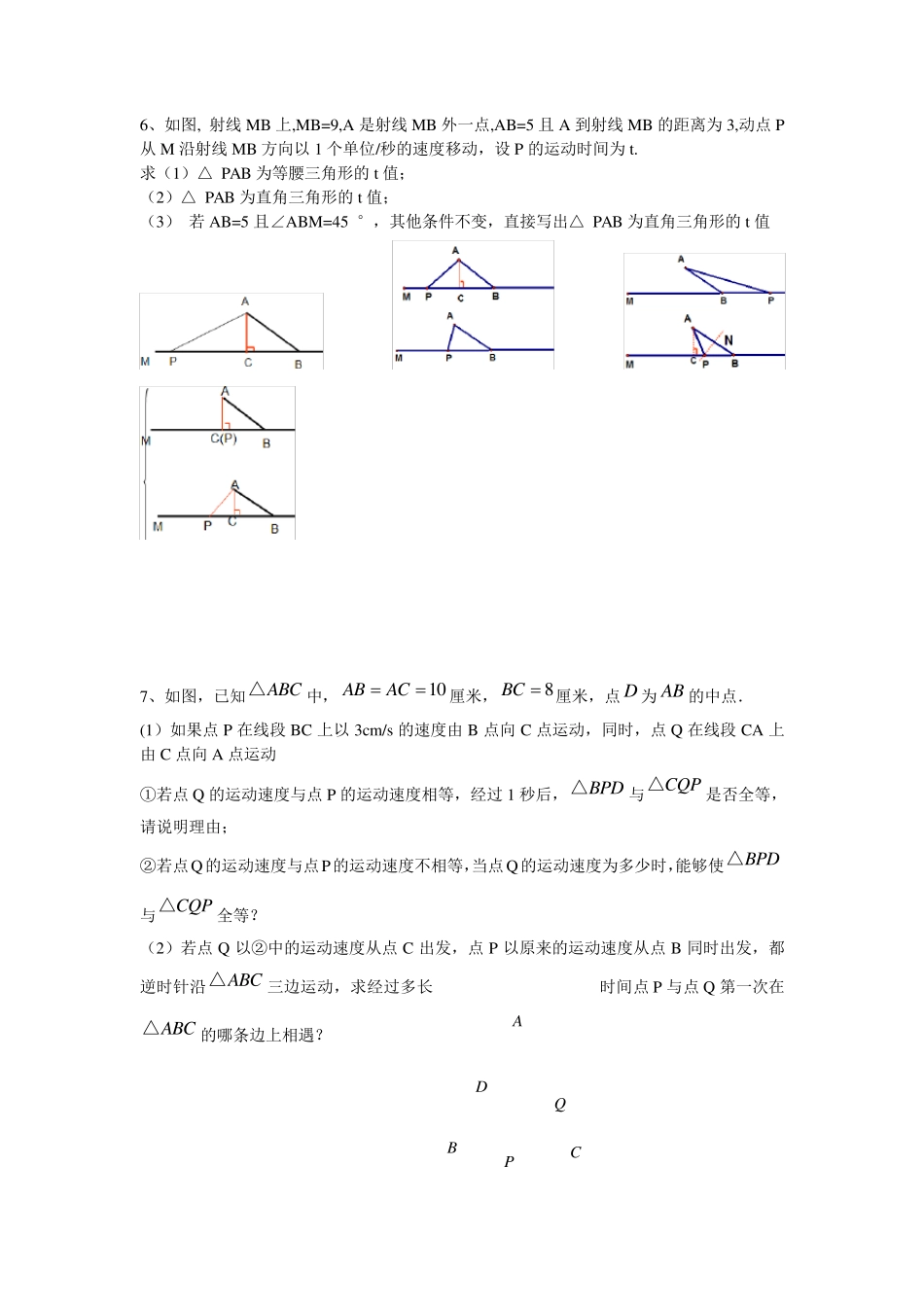
初二数学动点专题训练 1、如图1,梯形ABCD 中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿 AD 边以 1cm/秒的速度移动,点Q 从 C 开始沿 CB 向点B 以 2 cm/秒的速度移动,如果 P,Q 分别从 A,C 同时出发,设移动时间为 t秒。 当 t= 时,四边形是平行四边形; 当 t= 时,四边形是等腰梯形. 2、如图2,正方形ABCD 的边长为 4,点M 在边 DC 上,且 DM=1,N 为对角线 AC 上任意一点,则 DN+MN 的最小值为 . 3、如图,在Rt ABC△中,9060ACBB°, °,2BC .点O 是 AC 的中点,过点O 的直线l从与 AC 重合的位置开始,绕点O 作逆时针旋转,交 AB 边于点D .过点C 作CEAB∥交直线 l于点E ,设直线l的旋转角为 . (1)①当 度时,四边形EDBC 是等腰梯形,此时 AD 的长为 ; ②当 度时,四边形EDBC 是直角梯形,此时 AD 的长为 ; (2)当90 °时,判断四边形EDBC 是否为菱形,并说明理由. O E C B D A l O C B A (备用图) 4、在△ABC 中,∠ACB=90°,AC=BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN于E. (1)当直线MN 绕点C 旋转到图1 的位置时,求证:①△ADC≌△CEB;②DE=AD+BE; (2)当直线MN 绕点C 旋转到图2 的位置时,求证:DE=AD-BE; (3)当直线MN 绕点C 旋转到图3 的位置时,试问DE、AD、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明. 5、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF,且EF 交正方形外角DCG的平行线CF 于点F,求证:AE=EF. 经过思考,小明展示了一种正确的解题思路:取AB 的中点M,连接ME,则AM=EC,易证AMEECF△≌△,所以AEEF. 在此基础上,同学们作了进一步的研究: (1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除 B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除 C 点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由. A D F C G E B 图1 A D F C G E B 图3 A D F C G E B 图2 C B A E...