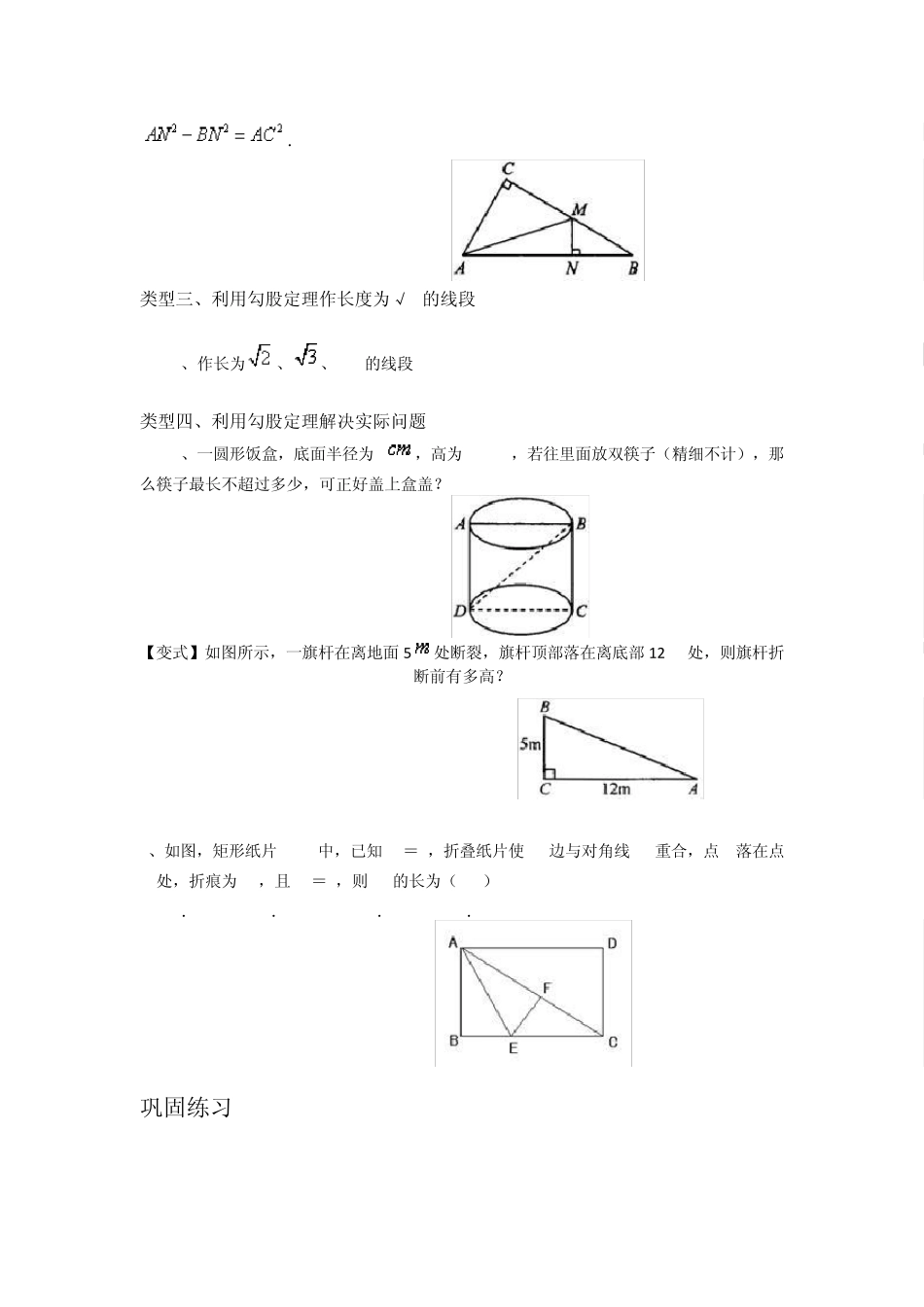
勾股定理 勾股定理(基础) 学习目标 1. 掌握勾股定理的内容及证明方法,能够熟练地运用勾股定理由已知直角三角形中的两条边长求出第三条边长. 2. 掌握勾股定理,能够运用勾股定理解决简单的实际问题,会运用方程思想解决问题. 3. 熟练应用勾股定理解决直角三角形中的问题,进一步运用方程思想解决问题. 要点梳理 要点一、勾股定理 直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为, 那么. 要点诠释: (1)勾股定理揭示了一个直角三角形三边之间的数量关系. (2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的. (3)理解勾股定理的一些变式:,, . 要点二、勾股定理的证明 方法一:将四个全等的直角三角形拼成如图(1)所示的正方形. 图(1)中,所以. 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形. 图(2)中,所以. 方法三:如图(3)所示,将两个直角三角形拼成直角梯形. ,所以. 要点三、勾股定理的作用 1. 已知直角三角形的任意两条边长,求第三边; 2. 用于解决带有平方关系的证明问题; 3. 利用勾股定理,作出长为的线段. 典型例题 类型一、勾股定理的直接应用 1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为、、. (1)若=5,=12,求; (2)若=26,=24,求. 【变式】在△ABC 中,∠C=90°,∠A、∠B、∠C 的对边分别为、、. (1)已知=2,=3,求; (2)已知,=32,求、. 类型二、勾股定理的证明 2、如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,试说明. 类型三、利用勾股定理作长度为√n的线段 3、作长为、、的线段. 类型四、利用勾股定理解决实际问题 4、一圆形饭盒,底面半径为8,高为12 ,若往里面放双筷子(精细不计),那么筷子最长不超过多少,可正好盖上盒盖? 【变式】如图所示,一旗杆在离地面 5处断裂,旗杆顶部落在离底部 12处,则旗杆折断前有多高? 5、如图,矩形纸片 ABCD中,已知 AD=8,折叠纸片使 AB边与对角线 AC重合,点 B落在点F 处,折痕为AE,且 EF=3,则 AB的长为( ) A.3 B.4 C.5 D.6 巩固练习 一.选择题 1. 在△ABC中,AB=12,AC=9,BC=15,则△ABC的面积等于( ) A. 108 B. 90 C. 180 D. 54 2.若直角三角形的三边长分...