利用几何知识求函数最值

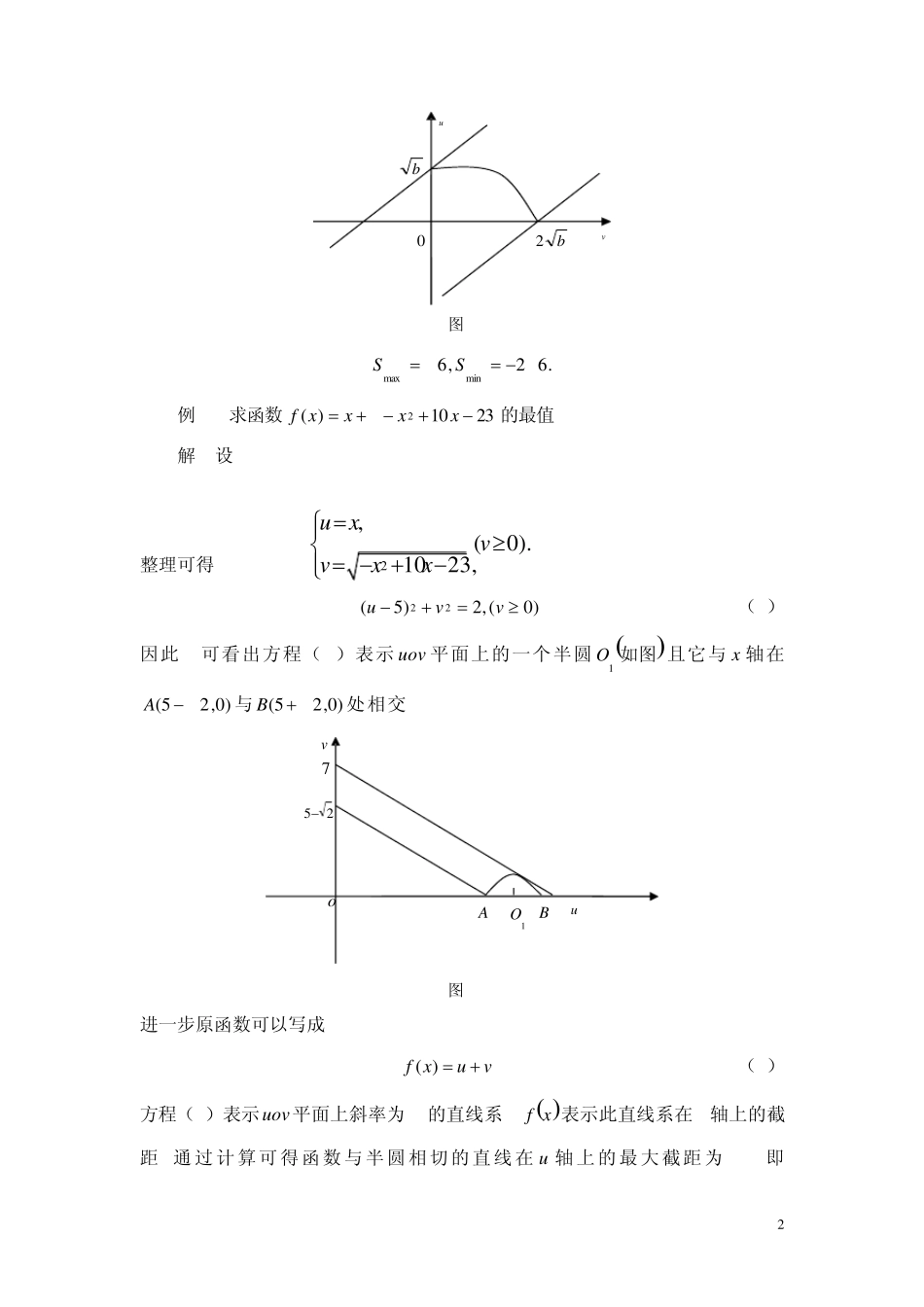
1 丁长青 编 1. 数形结合法 1.1 利用数轴上的截距解函数最值 截距是指函数与所有坐标轴交点的坐标之差, 可取正数也可取负数或0 .求形如)()(xgxfy的函数最值, 可以把)(),(xgxf当作是变量, 即令)(),(xguxfv, 方程0),(vuF一 般 表 示 一 条 曲 线 , 则 y 可以当作是yuv的直线在纵坐标轴上的截距, 因此截距的最值也即是函数的最值.]1[ 例 1 已知数yx,满足03422xyx, 求yx的最值. 解 令 ,byx则.bxy 因为1)2(22yx的圆心为)0,2(, 以及它到直线bxy的距离为1, 所以111|12|22b, 可得22 b. 于是 ,22maxb .22minb 例 2 求函数3424322ttttS的最值. 解 令,43,34222ttyttx 有 xyS又 ).0,0(,1624433422222yxyxttyttx 因此 S 可看成是直线系Sxy和椭圆162422 yx在第一象限相交直线在轴上的截距（如图所示）, 可得 2 b0b2uv 图1 .62,6minmaxSS 例3 求函数2310)(2xxxxf的最值. 解 设 整理可得 )0(,2)5(22vvu. （1） 因此, 可看出方程（1）表示uov 平面上的一个半圆如图1O且它与 x 轴在)0,25( A与)0,25( B处相交. v725oA1OBu 图2 进一步原函数可以写成 vuxf)(, （2） 方程（2）表示uov平面上斜率为-1的直线系,  xf表示此直线系在 u轴上的截距,通过计算可得函数与半圆相切的直线在 u 轴上的最大截距为 7, 即2,(0).1023,u xvvxx   3 7)(max xf而过)0,25( A直线在u 轴上 的 最 小 截 距 为,25  即25)(minxf 1.2 利用两点间的距离公式解函数最值 两点间的距离公式分为平面和空间两种形式, 在平面内设1122( ,),(,),A x yB xy则 122212||()() .ABxxyy 在空间中, 可设111222( ,,),(,,),A x y zB xyz 则 222121212||()()() .ABxxyyzz 例 4 求函数2225625()yxxxxxR的最小值. 解 如图所示. B 图 3 由于 2565222xxxxy 2222(1 )( 02 )(3 )( 04 )xx, 且 y 是点 ( ,0)x到点 (1,2),( 3,4)AB 的距离之和, B 关于 x 轴的对称点为( 3, 4)B, 因此 22(13)(24)2 13AB . 故 132max y. 4 例5 已知:如...