利用直线倾斜角求椭圆焦半径Word版含解析(数理化网)

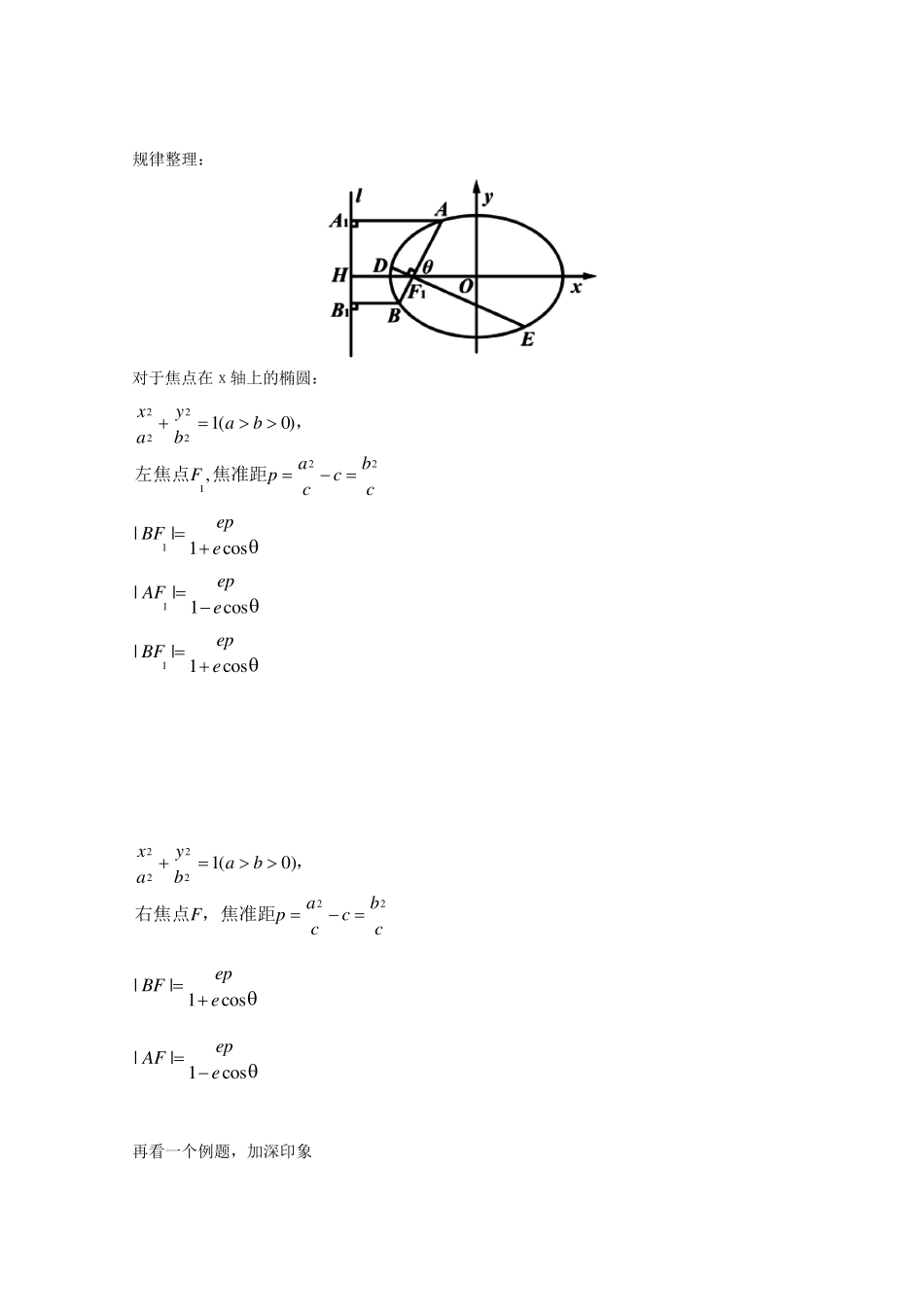
今天我们研究利用直线倾斜角求椭圆焦半径.根据椭圆的第二定义，可以推导出椭圆焦半径含倾斜角的公式，而且当倾斜角为直角时，焦点弦最短。 先看例题： 例：已知椭圆C:22221xyab(a＞b＞0),其相应于焦点F(2,0)的准线方程为x=4.已知过点F1(－2,0)倾斜角为θ 的直线交椭圆C 于A,B 两点,求证:24 2|| 2cosAB; 解： 根据题目条件，可知22222,4,cacabc∴可以解得：228,4.ab ∴椭圆C 的方程为22184xy .离心率22e  又 F1(－2,0)是椭圆C 的左焦点，设 l 为椭圆的左准线,则 l:x=－4. 作 AA1⊥l 于A1,BB1⊥l 于B1,l 与 x 轴交于点H(如图). 点A 在椭圆上, ∴112||||2AFAA 112 (|| ||cos )2F HAF122||cos2AF. ∴12||2cosAF. 同理：12||2cosBF. ∴|AB|=|AF1|+|BF1| 222cos2cos 24 22cos . 另解：当2时,记k=tanθ.则 AB:y=k(x+2), 将其代入方程 x2+2y2=8 得(1+2k2)x2+8k2x+8(k2－1)=0. 设 A(x1,y1),B(x2,y2), 则 x1,x2是此二次方程的两个根. 2122812kxxk  ,21228(1)12kxxk. 221212||()()ABxxyy 2212(1)()kxx 221212(1)[()4]kxxxx 222222832(1)(1)[()]1 21 2kkkkk. 224 2(1)12kk.① k2=tan2θ,代入①式得24 2|| 2cosAB.② 当2时,|| 2 2AB 仍满足②式. ∴24 2|| 2cosAB. 注意：另解思考上更直接，但明显运算量较大。 规律整理： 对于焦点在x 轴上的椭圆： 22222211(0),xyabababFpccc，左焦点焦准距 1|| 1cosepBFe  1|| 1cosepAFe  1|| 1cosepBFe  2222221(0)xyabababFpccc，右焦点，焦准距 || 1cosepBFe  || 1cosepAFe  再看一个例题，加深印象 例：已知椭圆C：22221(0)xyabab的离心率为32 ，过右焦点F 且斜率为k(k>0)的直线l 与椭圆C 相交于A，B 两点，若3AFFB，则k=________ 解：根据前面的公式，分别表示出 || 1cosepAFe ，|| 1cosepBFe  根据题意有：31cos1cosepepee 所以3cos3  进而tan2 2k  总结： 1.椭圆的焦点在x 轴上，利用直线倾斜角可以直接写出椭圆焦半径。 2.本文的公式都是以倾斜角为锐角的情形推导的，若倾斜角为直角或者钝...