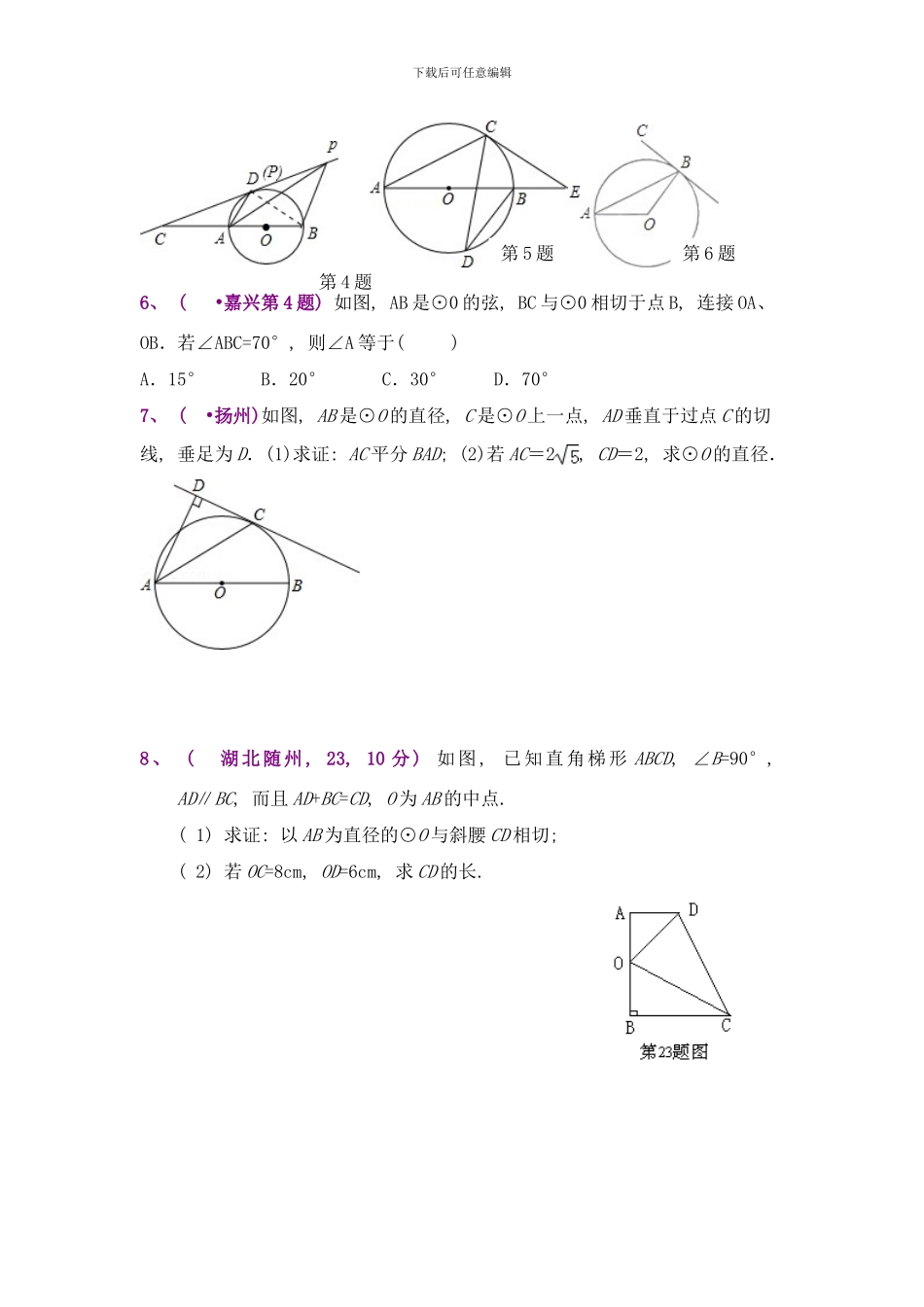
下载后可任意编辑辅导: 圆的切线( 一) 学习要求: 【学习目标】1.了解切线的概念, 探究切线与过切点的半径之间的关系.2.能判定一条直线是否为圆的切线, 理解切线的判定定理、 性质定理.3.会过圆上点画圆的切线.【学习重点】切线判定定理、 性质定理的区别与应用.( 二) 知识要点: 1. 直线是圆的切线.2.直线 与⊙O 相切于点 A, OA 是过切点的半径, 直线 与半径 OA 位置关系如何? 圆的切线 经过 的半径.( 三) 例题展现: 问题 1: ( •衢州第 21 题) 如图, 在 Rt△ABC 中, ∠C=90°, ∠ABC 的平分线交 AC 于点 D, 点 O 是 AB 上一点, ⊙O 过 B、 D 两点, 且分别交 AB、 BC 于点 E、 F.( 1) 求证: AC 是⊙O 的切线; ( 2) 已知 AB=10, BC=6, 求⊙O 的半径 r.[来源:学,科,网 Z,X,X,K]问题 2: ( •丽水第 20 题)如图, AB 为⊙O 的直径, EF 切⊙O 于点 D, 过点 B 作BH⊥EF 于点 H, 交⊙O 于点 C, 连接 BD.下载后可任意编辑(1)求证: BD 平分∠ABH; (2)假如 AB=12, BC=8, 求圆心 O 到 BC 的距离.( 四) 自我体会: 1、 ( 山东省荷泽市, 11, 3) 如图, PA、 PB 是⊙o 的切线, A、 B 为切点, AC 是⊙o 的直径, 若∠P=46 , ∘则∠BAC=______.2、 ( •扬州)如图, PA、 PB 是⊙O 的切线, 切点分别为 A、 B 两点, 点 C 在⊙O 上, 假如 ACB=70°, 那么∠P 的度数是 .3、 ( 海南) 如图, ∠APB=300, 圆心在边 PB 上的⊙O 半径为 1cm, OP=3cm, 若⊙O 沿 BP 方向移动 , 当⊙O 与直线 PA 相切时 , 圆心 O 移动的距离为 cm.4、 ( •黄石) 如图( 4) 所示, 直线与线段为直径的圆相切于点, 并交的延长线于点, 且, , 点在切线上移动.当的度数最大时, 则的度数为( ) A. ° B. ° C. ° D. °5、 ( 山西, 9, 2 分) 如图, AB 是⊙O 的直径, C.D 是⊙O 上一点, ∠CDB=20°, 过点 C 作⊙O 的切线交 AB 的延长线于点 E, 则∠E 等于( ) A. 40° B. 50° C.60°D.70°第 1 题第 2 题第 3 题下载后可任意编辑6、 ( •嘉兴第 4 题) 如图, AB 是⊙0 的弦, BC 与⊙0 相切于点 B, 连接 OA、 OB.若∠ABC=70°, 则∠A 等于( ) A.15° B.20° C.30° D.70°7、 ( •扬州)如图, AB 是⊙O 的直径, C 是...