动力学习题库新

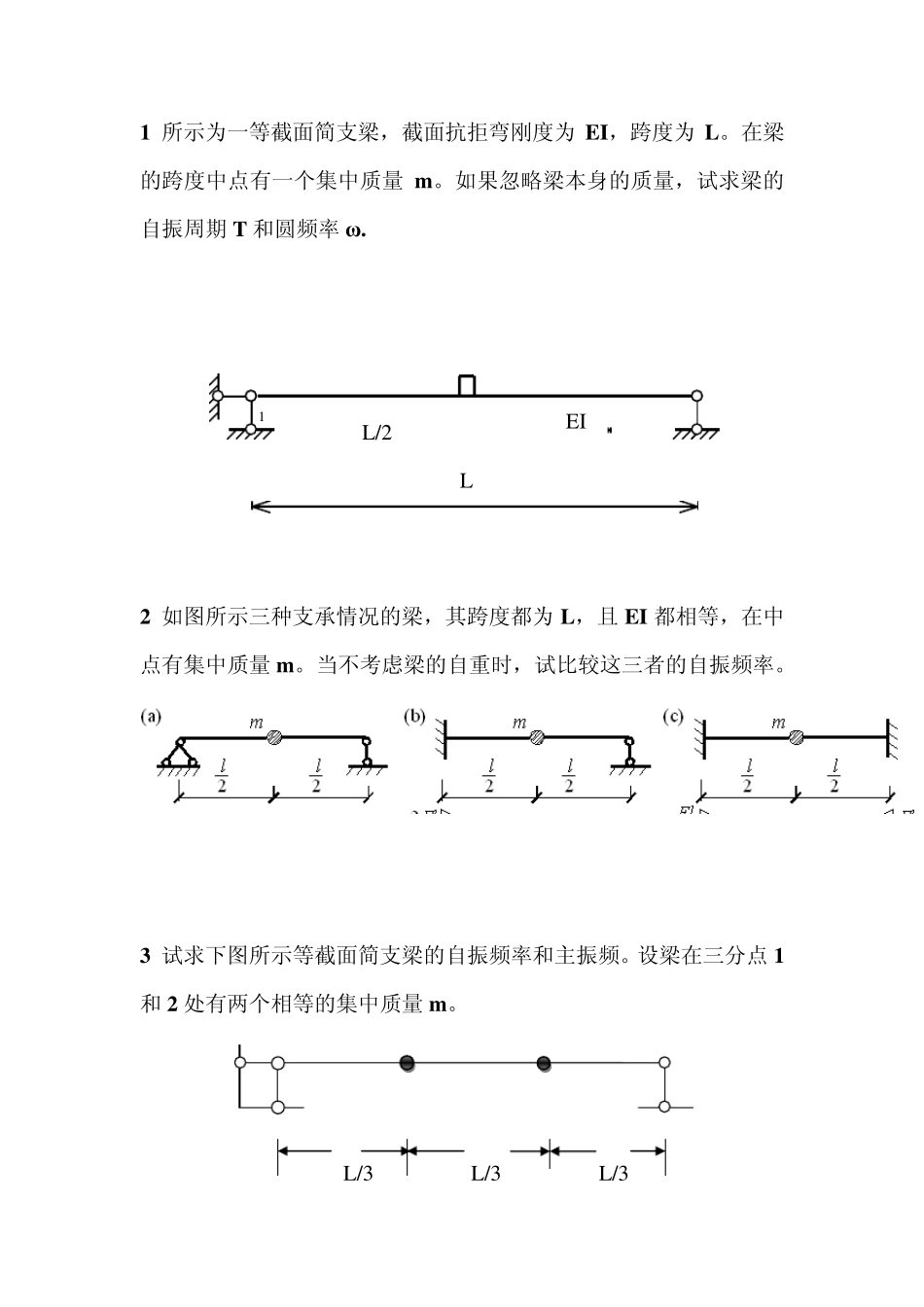
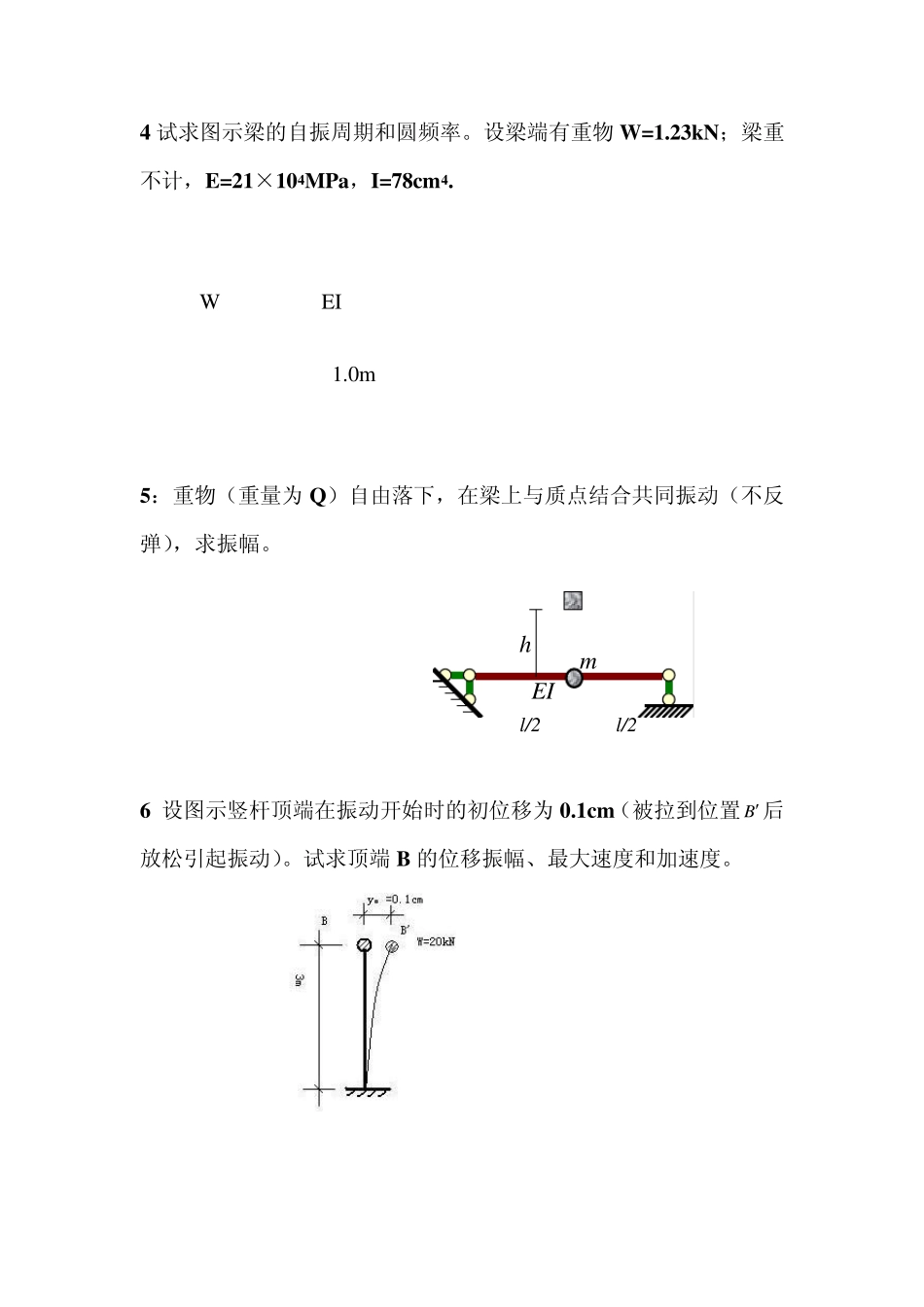
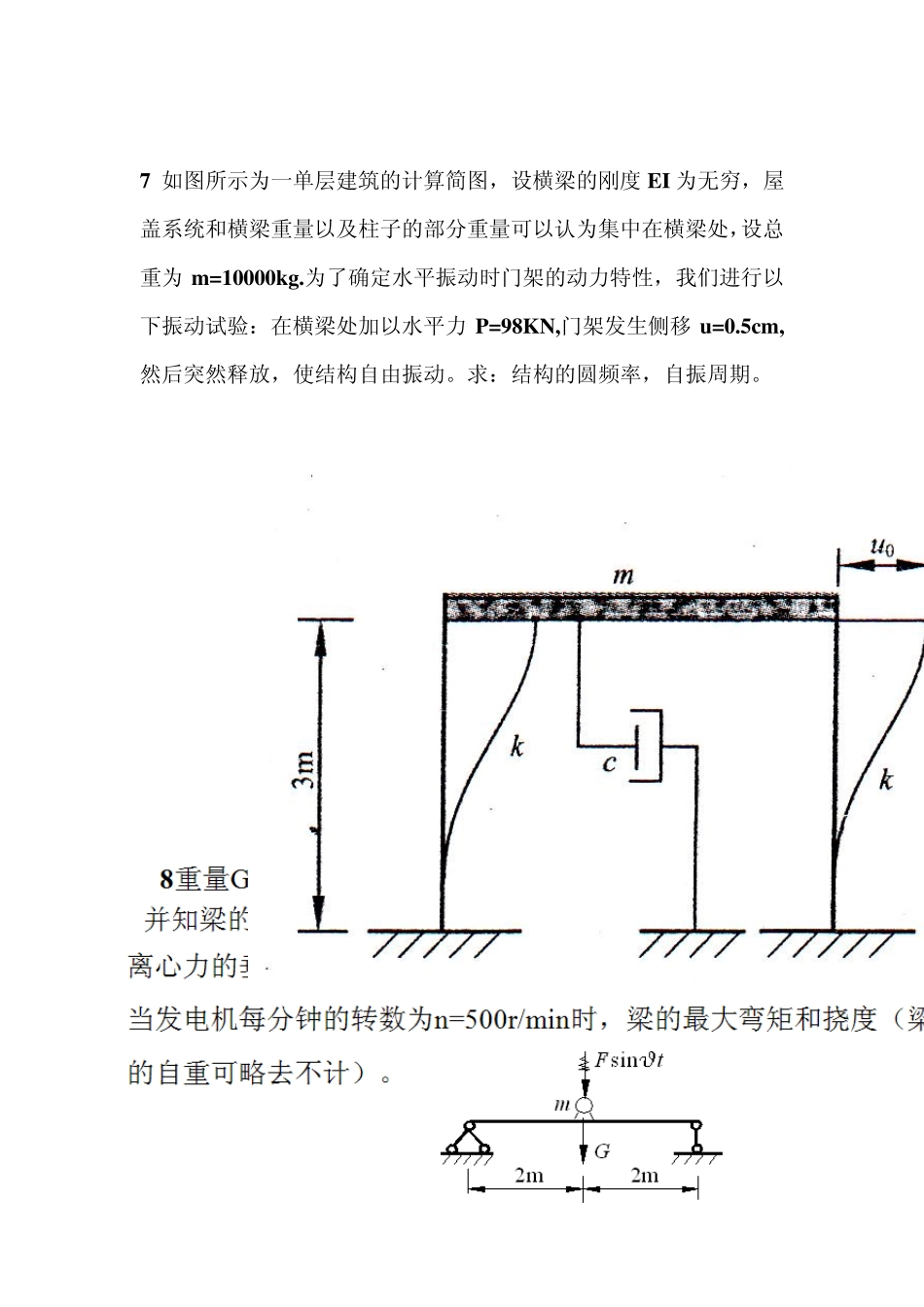
1 所示为一等截面简支梁，截面抗拒弯刚度为EI，跨度为L。在梁的跨度中点有一个集中质量 m 。如果忽略梁本身的质量，试求梁的自振周期 T 和圆频率 ω. 2 如图所示三种支承情况的梁，其跨度都为L，且 EI 都相等，在中点有集中质量 m 。当不考虑梁的自重时，试比较这三者的自振频率。 3 试求下图所示等截面简支梁的自振频率和主振频。设梁在三分点 1和 2 处有两个相等的集中质量 m 。 L /3 L /3 L /3 L /2 L EI 1 m EI l/2 l/2 h 4 试求图示梁的自振周期和圆频率。设梁端有重物W=1.23kN；梁重不计，E=21×104MPa，I=78cm 4. W EI 1.0m 5：重物（重量为 Q）自由落下，在梁上与质点结合共同振动（不反弹），求振幅。 6 设图示竖杆顶端在振动开始时的初位移为 0.1cm（被拉到位置 B后放松引起振动）。试求顶端B 的位移振幅、最大速度和加速度。 7 如图所示为一单层建筑的计算简图，设横梁的刚度EI 为无穷，屋盖系统和横梁重量以及柱子的部分重量可以认为集中在横梁处，设总重为m=10000kg.为了确定水平振动时门架的动力特性，我们进行以下振动试验：在横梁处加以水平力P=98KN,门架发生侧移u=0.5cm,然后突然释放，使结构自由振动。求：结构的圆频率，自振周期。 9 试求图示梁的最大竖向位移和梁端弯矩幅值，已知 W=10KN，Fp=2.5KN，E=2 105MPa,I=1130cm4,θ=57.6s-1,L=150cm. Fp(t)=Fpsinθt A W L 1 解：对于简支梁跨中质量  =L3 /48EI T=2πm=2πEIm48/L3 W=1/m=3/48m LEI 2 3解 先求柔度系数。为此，作、图如图 10-35b、b 所示。由图乘法求得 1 2L/9 1 2L/9 δ11=δ12= 然后代入式（10-45），得 从而求得两个自振圆频率如下： 最后求主震动型。由式（10-46a、b），得 = = 4 解：悬臂梁的柔度系数  L3/3EI T=2π/Wg=2π3 / 3WLEIg =2π4141.23/321 101078 109.8 =0.1008s  =2π/T=2π/0.1008=62.3s-1 5 解：为一般动力荷载下单自由度体系强迫振动 y（t）= s=mv δ= ω = y max==(可化简) 6 6 解：m/1k/m  由图乘法得NmEIAy/103291010161010223321/684640 1637.411032910208.9//1sWgm B 端的位移振幅即为初位移0.1cm 为只有初位移的无阻尼单自由度体系，y（t）=y 0 V0=0，则y（t）=y 0 y（t）=0.1 速度tyyv7.41sin17.4)( scmv/17.4max  加速度ttvtya7.41cos9.173)()( 2max/9.173scma 综上即： 2maxmaxmax/9.173/7.411.0scmascmvcmy 10 解：依题知 k=P∕u=98000/0.005=19600000 圆频率 w=10471096.1 =44.2719rad/s 自振周期 T=2πw=23.1444.2719=278.03 12.解：体系柔度系数 δ= ω====44.73s-1 最大静位移 yst=Fpδ==0.1244cm 最大竖向位移 ymax=yst ==−0.182cm βmax===−0.1463 MAmax=(β∙Fp+W)L=（1.4632.5+10）150=20.49KN∙m