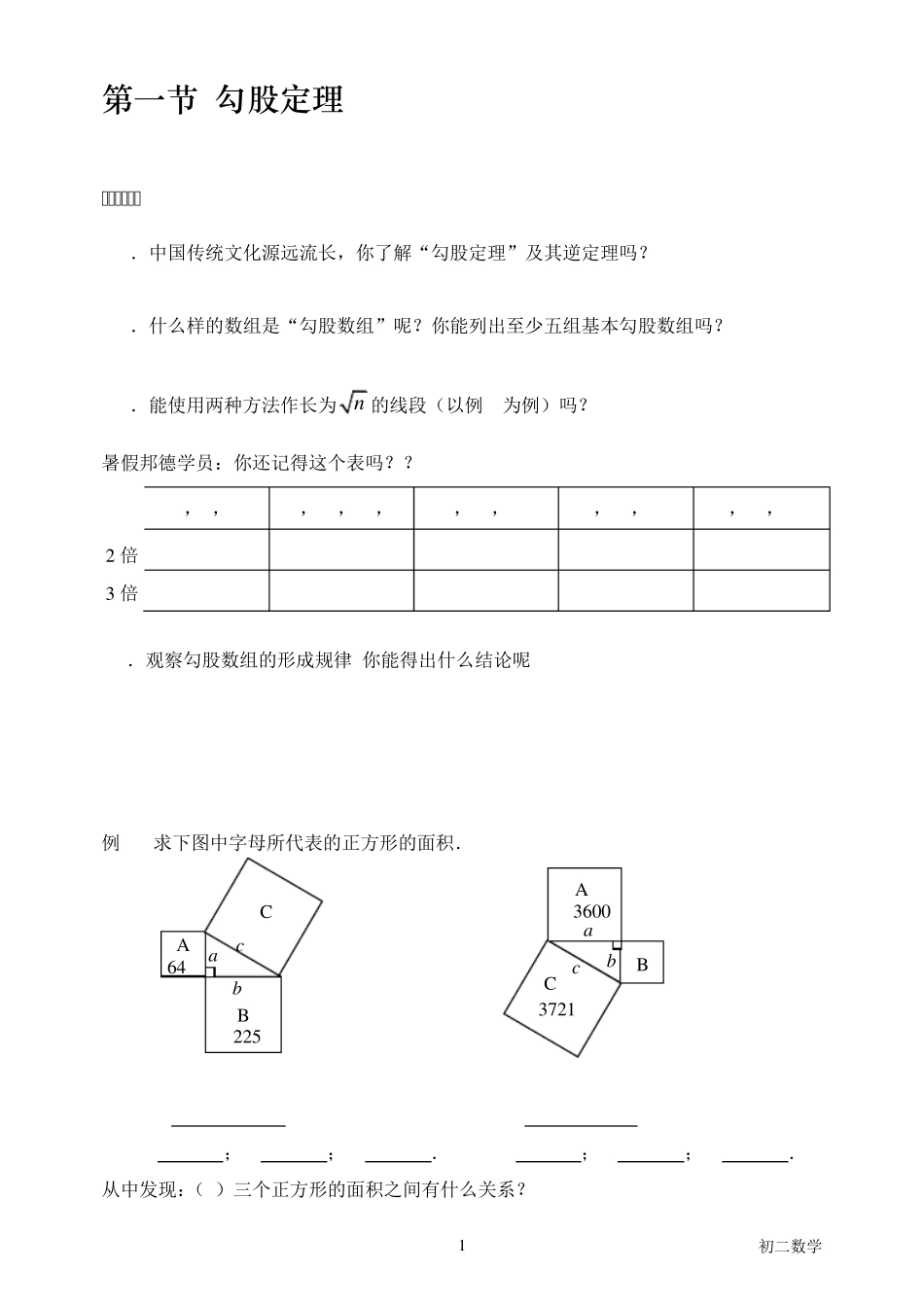
初二数学 1 第一节 勾股定理 【知识要点】 1.中国传统文化源远流长,你了解“勾股定理”及其逆定理吗? 2.什么样的数组是“勾股数组”呢?你能列出至少五组基本勾股数组吗? 3.能使用两种方法作长为n 的线段(以例 6为例)吗? 暑假邦德学员:你还记得这个表吗?? 3,4,5 5,12,13, 7,24,25 8,15,17 9,40,41 4.观察勾股数组的形成规律,你能得出什么结论呢? 例 1 求下图中字母所代表的正方形的面积. SC= SB= a= ;b= ;c= . a= ;b= ;c= . 从中发现:(1)三个正方形的面积之间有什么关系? 2 倍 3 倍 C A 225 64 a b c B A 3600 C 3721 B a c b 初二数学 2 (2)三个正方形围成的直角三角形三边长度之间有什么关系? 【典型例题】 例1 直角三角形的周长为30cm,斜边长为13cm,那么这个三角形的面积为多少? 例2 如图,已知△ABC中,AD、AE分别是BC边上的高和中线,AB=9cm ,AC=7cm ,BC=8cm ,求DE的长. 例3 已知△ABC中,AB=AC,AB=6cm,BC=4cm. 求(1)S△ABC; (2)腰AC上的高BE. 例4 在钝角三角形ABC中,CB=9cm,AB=17cm,AC=10cm,AD⊥BC的延长线于 D,求AD的长. B D A C A C D E B 初二数学 3 例3 如图,四边形ACDE是长方形,它的面积是239m ,CD=3m,AB=5m,∠ABC=90 ,求以 BC为直径的半圆的面积(结果保留 )。 例5 如图,在点 D处有甲、乙二人同时出发,甲沿 DA、AB过桥到达点 B处,乙沿 DC过桥由 C点直达点 B处.已知 DA=6里,AB=6里,DC=2里.假设甲、乙二人速度相同,问甲、乙二人谁先到达点 B处?说明理由. 例5 如图所示,在△ABC中,AB=9,AC=6,AD⊥BC于点 D,M为 AD上任一点,求 MB2-MC2的值. 例6 在数轴上用点表示:2 A E D C B 初二数学 4 例7 如图所示,B点在AC上,且AB:BC=1:2,△ABD和△BCE都是等边三角形,求证:∠EDB=90° 例8 如图,四边形ABCD中,∠ABC=135°,∠BCD=120°,AB=6 ,BC=53,CD=6, 求AD的长. 例9 如图,已知△ABC中,AB=AC,P是边BC上的一点.求证:AB2=AP2+BP·PC 大显身手 A B C D E A B C P 初二数学 5 姓名: 成绩: 1.若直角三角形三边长为三个连续偶数,则它的三边长为( ) A.2,4,6 B.4,6,8 C.6,8,10 D.8,10,12 2.在直角三角形ABC中,∠C=90°,AC=48,BC=7,AC边上中线 BD的长为( ) A.24 B...