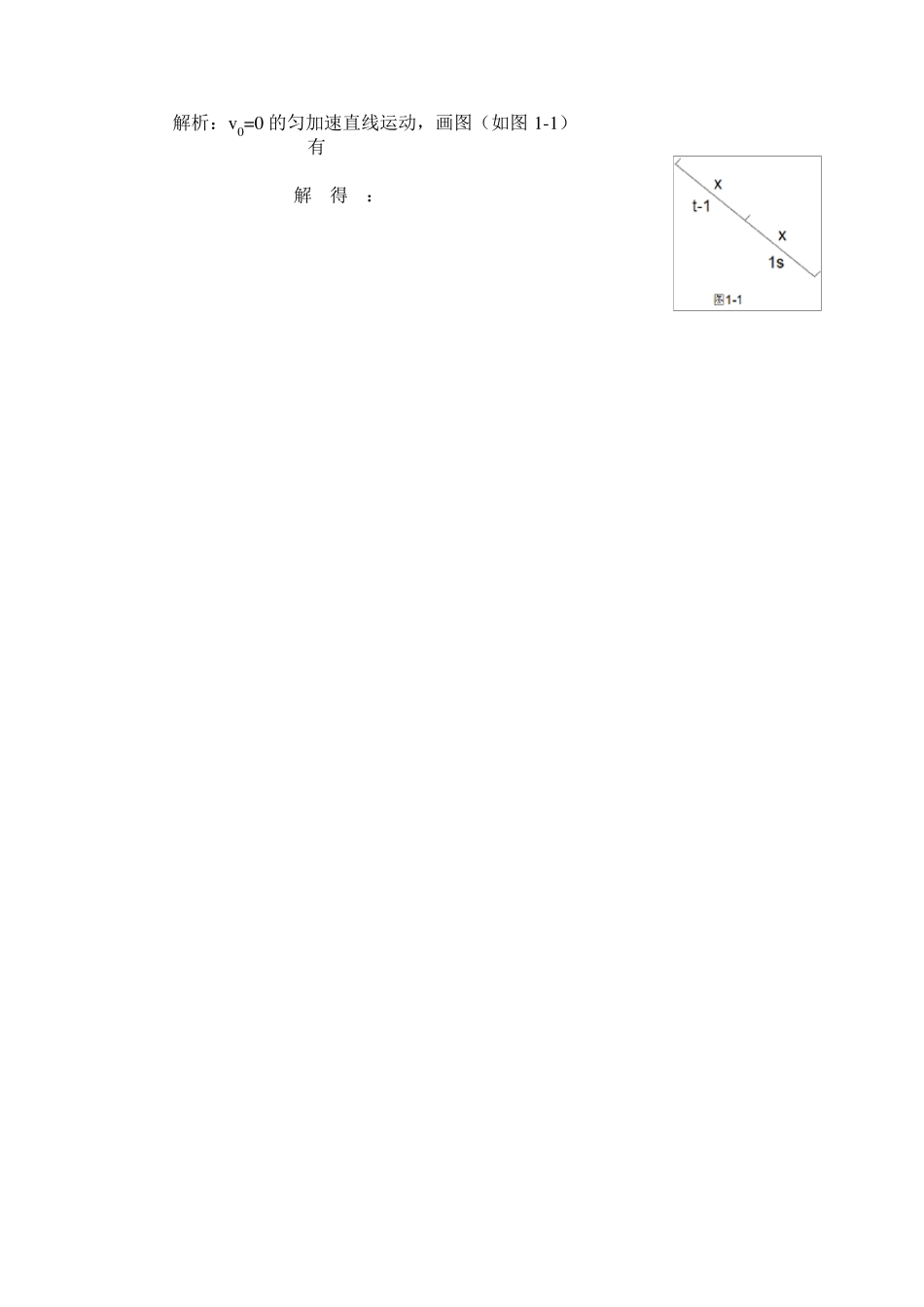
第一部分 匀变速直线运动 I、知识要点 1、基本公式 2、典型推论 1)当 v 0=0,有、即 其中各个量的物理意义如图 1-1 所示 2)若连续两端运动的时间都为 t,位移分别为 x 1、x 2,则有: x 2-x 1=at2 3、运动图像(绝对值表示大小、正负表示方向) 1)x -t 图像 纵坐标:物体所在位置的坐标 斜率:瞬时速度 2)v -t 图像 纵坐标:瞬时速度 斜率:加速度 与横轴围成的面积:位移 3)a-t 图像 纵坐标:加速度 与横轴围成的面积:速度的变化量 II、题型分类及解决方案 1、单体运动 解决方案: 1)画图 2)分段、标已知条件 3)设未知公共量 4)列方程 2、追击相遇问题 解决方案: 相遇问题的解决方案与单体运动类似,追击问题的解决方案如下: 1) 先由题中问法分类 2)①“一定追得上”问题:解法同相遇问题 ②“判断能否追上”问题:假设可以追上,按相遇问题计算时间。若有解,则可以追上;若无解,则不能追上。 ③“为确保追上,应如何”问题:速度相等时,恰好相遇 3、v 0=0 的匀加速直线运动 1)根据题意将题中运动分成至少两段 2)使用进行求解。 4、在纸带上求解加速度和速度 1)先得到每段运动所需时间 t 2)求速度,例 3)求加速度 求加速度时,若纸带上有偶数段运动,则直接使用上述求 a 的式子,若有奇数段运动,则舍去位移最小的一段,变成偶数段后再使用上式计算。 5、图像问题 1)利用画图像解决变加速运动 2)在给定图像中求解加速度、速度、位移 6、有关减速运动问题 1) 讨论是否停下来 以下两种情况不需要讨论是否停下来,直接列方程解决 ① 已知问题发生时刻物体是否已经停下 ② 物体停下后立即以相同的加速度反向加速运动(比如竖直上抛运动) 2) 方程中正方向的选取 方程中原有的符号不能改变,所有已知量和所设未知量的字母都只表示大小,在前面添加正负号来表示方向。若所设未知量方向未知,则需假设方向:若求解后结果为正,则与假设方向相同;反之相反。 III 例题赏析 例 1、物体从光滑的斜面顶端由静止开始匀加速下滑,在最后 1s 内通过了全部路程的一半,则下滑的总时间为______s 解析:v0=0 的匀加速直线运动,画图(如图 1-1) 有 解得: 例2、一物体做匀减速直线运动,加速度为-2 m/s2。该物体在某 1 s 内的位移为 6m,此后它还能运动多远? 解析:单体的匀加速直线运动 1) 画图(如图 1-2) 2) 标上已知条件...